Single Degree of Freedom (SDOF) Systems
Consider the simple mass-spring system. The mass (m) is subjected to a force F(t) in the u direction as, a function of time. The mass is allowed to move in the u direction only and hence this is a Single-Degree-Of-Freedom (SDOF) system. The motion is resisted by a spring of stiffness (k)
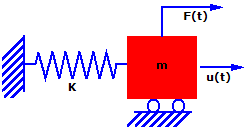
Writing Newton's Second Law (force equals mass times acceleration) for this system at time (t) results in:
F(t) - ku(t) = mu..(t)
or:
mu..(t) + ku(t) = F(t)
where:
u..(t) is the acceleration of the mass at time (t) and it is equal to the second derivative of u with respect to time
k = is the stiffness of the spring
Theoretically, if the mass is displaced and released, it will continue to vibrate with the same amplitude forever. In practice, the mass vibrates with progressively smaller amplitudes until it comes to rest. This phenomenon is called damping and it is caused by loss of energy through friction and other effects. Damping is a complex phenomenon. For the purpose of this discussion, assume that the damping force is proportional to the velocity. This type of damping is called viscous damping.

Considering damping, the above equation becomes:
mu..(t) + cu.(t) + ku(t) = F(t)
where:
u.(t) is the velocity of the mass at time (t), and it is equal to the first derivative of u with respect to time
In static studies, velocity and acceleration are so small that they can be neglected and F and u are not functions of time. The above equation reduces to: F=ku.
Multi Degree of Freedom (MDOF) Systems
For a Multi-Degree-of-Freedom (MDOF) system, m, c, and k become matrices instead of single values and the equations of motion are expressed as:
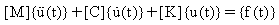
where:
[M]: mass matrix
[K]: stiffness matrix
[C]: damping matrix
{u(t)}: displacement vector at time t (displacement components of every node)
 : acceleration vector at time t (acceleration components of every node)
: acceleration vector at time t (acceleration components of every node)
 : velocity vector at time t (velocity components of every node)
: velocity vector at time t (velocity components of every node)
{f(t)}: time varying load vector (force components of every node)