In linear static analysis, the loads are applied gradually and slowly until they reach their full magnitude. After reaching their full magnitude, the loads remain constant (time-invariant). The accelerations and velocities of the excited system are negligible, therefore, no inertial and damping forces are considered in the formulation:

where:
[K]: stiffness matrix
{u}: displacement vector
{f}: load vector
The solution produces displacements, stresses, that are constant.
In linear dynamic analysis, the applied loads are time-dependent. The loads can be deterministic (periodic, non-periodic), or non-deterministic which means that they cannot be precisely predicted but they can be described statistically. The accelerations and velocities of the excited system are significant, therefore, inertial and damping forces should be considered in the formulation:
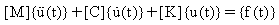
where:
[K]: stiffness matrix
[C]: damping matrix
[M]: mass matrix
{u(t)}: time varying displacement vector
 : time varying acceleration vector
: time varying acceleration vector
 : time varying velocity vector
: time varying velocity vector
{f(t)}: time varying load vector
The response of the system is given in terms of time histories (amplitudes versus time), or in terms of frequency spectra (peak values versus frequency).
For linear dynamic analysis, the mass, stiffness, and damping matrices do not vary with time.
Material properties are assumed to be linear. Nonlinear dynamic studies must be used if material nonlinearity exists.
In general, you can assume static conditions if the frequency of the loads is much lower than the lowest natural frequency of the system.