Демпфирующие эффекты

Если вы примените начальные условия к динамической системе, система вибрирует с уменьшающейся амплитудой до тех пор, пока не наступит состояние покоя. Настоящее явление называется демпфированием. Демпфирование является комплексным явлением, которое рассеивает энергию посредством многих механизмов, подобных внутреннему и внешнему трению, термическим воздействиям циклических упругих напряжений материалов на микроскопическом уровне и сопротивлению воздуха.

Трудно описать механизм рассеяния математически. Демпфирующие эффекты (влияния демпфирования) обычно представлены идеализированными математическими формулами. Во многих случаях влияния демпфирования в достаточной степени описываются эквивалентными вязкими демпферами.

Вязкий демпфер (или амортизатор) создает силу, пропорциональную скорости. Поршень, который может свободно перемещаться внутри цилиндра, заполненного вязкой жидкостью, подобной маслу, является примером вязкого демпфера. Демпфирующая сила F_d принимается линейной по отношению к относительной скорости на двух концах демпфера:

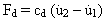(Уравнение 1).

Константа c_d, которая является наклоном кривой F_d по отношению к относительной скорости называется коэффициентом вязкостного демпфирования;

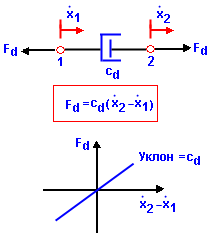
Единицы измерения коэффициента вязкостного демпфирования – (сила)/(скорость) или (сила x время)/(длину).

Реакция обычной системы с вязким демпфированием с n степенями свободы дается:

(Уравнение 2).

где:

[M] = n x n симметричная матрица масс (или инерции)

[C] = n x n симметричная матрица демпфирования

[К] = n x n симметричная матрицы жесткости

{f(t)} = n-мерный вектор силы

{u}, и являются n-мерными векторами перемещения, скорости и ускорения соответственно.

В общем, классический модальный анализ не обязательно приводит к системе независимых уравнений движения, кроме случаев, когда матрица демпфирования [c], получившаяся в результате модального преобразования координат, может рассматривается в качестве диагональной матрицы.

(Уравнение 3).