A partir de la courbe S-N de résistance à la fatigue d'un matériau donné, vous pouvez dériver les constantes de l'équation de Basquin ou laisser le programme calculer les constantes de Basquin en spécifiant le nombre de points de données sur la courbe S-N à inclure dans les calculs d'ajustement de la courbe.
Certains matériaux disponibles dans la base de données SOLIDWORKS Materials et sur le portail Web de SOLIDWORKS Materials possèdent des informations sur les données de courbe de fatigue S-N. Par exemple, la courbe S-N du matériau Ti-6AI-4V (Metal_Ti Alpha-Beta Alloy) téléchargée à partir du portail Web de SOLIDWORKS Materials (le format de la base de données de matériaux est *.sldmat) est indiquée à une échelle Log S-Log N.
Les valeurs numériques des quatre premiers points de données S-N sont données dans la table.

L'équation de Basquin est une relation de loi de puissance qui décrit la relation linéaire entre les cycles de contrainte appliqués (S) dans l'axe Y et le nombre de cycles requis pour entraîner une rupture dans l'axe X lors d'un tracé sur une échelle Log-Log.
Elle peut être définie ainsi :
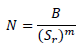
où N représente le nombre de cycles requis pour entraîner une rupture, généralement supérieur à 104, Sr est la valeur de référence de résistance à la fatigue (dans Simulation, il s'agit de l'amplitude de contrainte prise comme 2* la contrainte alternée), m est l'inclinaison de la courbe de résistance à la fatigue Log S-Log N, et B représente la valeur de la contrainte à un cycle.
Pour calculer l'inclinaison m de l'équation de Basquin, résolvez le système d'équations :

Pour résoudre m, utilisez le Log des deux expressions :
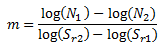
En substituant les deux premiers points de données S-N dans la table ci-dessus, calculez d'abord m, puis B :
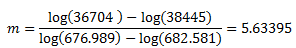

Pour la constante B, le programme prend en compte la valeur de l'amplitude de contrainte (de la contrainte cyclique maximale à la contrainte cyclique minimale). Si les valeurs de contrainte de la courbe S-N sont données en tant que contraintes alternées (ce qui est la pratique commune), multipliez ces contraintes par 2 pour calculer la constante B (amplitude de contrainte = 2* la contrainte alternée, en supposant une contrainte de moyenne nulle et une inversion complète du chargement cyclique). Si les données de la courbe S-N sont données dans des valeurs d'amplitude de contrainte, appliquez-les directement dans l'équation pour évaluer la constante B. Pour le calcul de la constante d'inclinaison m, la multiplication des contraintes ne modifie pas la valeur de l'inclinaison.
Dans l'onglet
Courbes de fatigue S-N (boîte de dialogue
Matériau), saisissez les valeurs de B dans
Constante spécifique à la courbe (B) et m dans
Inclinaison de la courbe S-N (m). Sélectionnez les unités de contrainte appropriées dans
Unités et désactivez l'option
Estimer les constantes de Basquin à partir de la courbe S-N.
Vous pouvez également trouver des tracés de courbes de résistance à la fatigue dans les codes tels que l'Eurocode 9 : Calcul de structures en aluminium : Structures sensibles à la fatigue, Réf. EN 1999-1-3:2007/A1.
Exemple de courbe S-N de résistance à la fatigue
Dans l'Eurocode 9, vous pouvez trouver des valeurs numériques pour la constante d'inclinaison m pour différentes catégories de détail, puis calculer B.
Par exemple, à partir de Réf. Table J.2 - Catégories de détail pour éléments soudés, EN 1999-1-3:2007/A1 pour une tôle simple avec des trous, la plage de contrainte Ds = 100 MPa à N = 2x106 cycles et l'inclinaison m = 7 ; B est alors égal à :
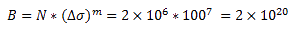
Pour laisser le programme effectuer l'ajustement de la courbe pour un ensemble spécifié de données S-N sur une ligne droite, sélectionnez Estimer les constantes de Basquin à partir de la courbe S-N. Dans ce cas, assurez-vous que Interpolation est défini sur Log-log et sélectionnez le dernier point de données S-N à prendre en compte pour l'ajustement de la courbe dans Envisager le point limite pour la courbe S-N à la ligne.
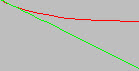
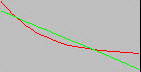
Les deux diagrammes présentent la superposition d'une courbe S-N d'origine (ligne rouge) avec la ligne d'ajustement de courbe de l'équation de Basquin (ligne verte) pour 2 (a) et 22 (b) points de données S-N, respectivement. Il est recommandé de vérifier la qualité de l'ajustement de courbe de Basquin avant de passer à l'analyse. La qualité de la ligne d'ajustement de courbe lors de l'approximation de la courbe S-N d'origine est la meilleure pour la portion de la courbe S-N jusqu'au point limite.
|
|
| (a) Ajustement de la courbe de Basquin avec 2 points de données S-N (ligne verte). |
(b) Ajustement de la courbe de Basquin avec 22 points de données S-N (ligne verte). |