Metodi di integrazione

I seguenti metodi di integrazione sono usati per gli studi di vibrazione random.

Metodo standard

Il metodo standard per l'analisi della vibrazione random procede nel modo seguente:
  1. alcuni punti di frequenza sono selezionati intorno ad ogni modalità naturale richiesta. Le ubicazioni di questi punti dipendono dal valore del parametro bias p.

    Per un parametro bias di 1.0, tutti i punti di frequenza sono distribuiti in modo uniforme tra le frequenze naturali. Se il parametro bias è maggiore di 1.0, i punti vengono selezionati più vicini alle frequenze naturali. I valori di default per i punti di frequenza e il parametro bias sono dati come funzione del primo rapporto di smorzamento ζ. Per una illustrazione sulla selezione dei punti di frequenza, fare clic qui.

    I valori di default per i punti di frequenza e il parametro bias come funzione di ζ sono elencati di seguito:

    Rapporto di smorzamento modale Numero di frequenze (Default) Parametro bias (Default)
    ζ < 0.01 21 11
    0.0,1 < ζ < 0.01 21-4.34 ln(ζ /0.01) 11-3.47 ln(ζ /0.01)
    ζ > 0.1 11 3

    Il software applica i valori di default dati nella Tabella 1 dove zero (0) è definito per il Numero di punti di frequenza e Parametro bias.

  2. Psd modali di responso sono valutati per ogni punto di frequenza. Il rapporto modalità trasversale-taglio (RAPPORTO) imposta un limite sul rapporto di tutte le possibili coppie di frequenze naturali (wi / wj, i > j).

    Ciò significa che per ogni coppia di modalità con wi / wj > RAPPORTO, i termini di densità spettrale trasversale sono ignorati. Gli effetti di modalità trasversale non sono considerati per RAPPORTO =1.

  3. I psd modali sono quindi integrati numericamente sul range di frequenza specificata per rallentare i valori medi al quadrato e le covarianze del responso modale. L'integrazione viene portata avanti numericamente usando l'integrazione Gauss dell'ordine 2 o 3 su ogni intervallo di frequenza in base ad un'interpolazione da log a log. Il responso medio al quadrato viene ottenuto sommando i contributi dell'intervallo.
  4. In conclusione, la trasformazione da modale a nodale rallenta gli spostamenti rms, le velocità e le accelerazioni del sistema.

Metodo approssimativo

Il metodo standard di integrazione può essere dispendioso in tempi a causa dell'integrazione numerica delle matrici ampie. Il metodo approssimativo d'integrazione effettua una soluzione semplificata facendo le seguenti considerazioni:
  • ignorando il responso di modalità trasversale, Sx(ω), questo è il risultato di una modalità sull'altra, ovvero

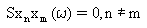    (Equazione 1)

  • Il psd delle eccitazioni è considerato costante intorno ad ogni modalità. Quindi, ogni modalità viene considerata eccitata dal "rumore bianco" con densità spettrale Sn, dove;

    (Equazione 2)

    ωn è la frequenza naturale della modalità n (n = 1,2,...nf).

    Per il rumore bianco, i responsi medi al quadrato possono essere determinati analiticamente per i responsi modali:

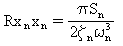    (Equazione 3)

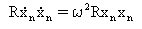    (Equazione 4)

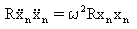     (Equazione 5).