粘性効果のため力学エネルギーを吸収できる弾性材料は、粘弾性材料と呼ばれます。
多軸応力状態では、この補助方程式を次のように記述できます:
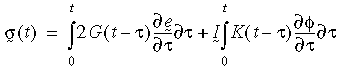
ここで、 e(bar)と φ は偏差ひずみと体積ひずみであり、G(t - τ)と K(t - τ)はせん断緩和関数と体積緩和関数です。
緩和関数は、通常は一般化 Maxwell モデルと呼ばれる力学モデルで表すことができ、次のように記述されます。
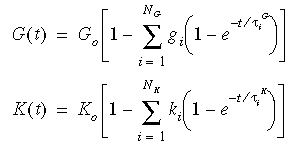
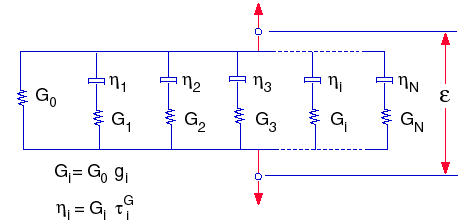
ここで、 G0 = E / 2(1+ ν)、初期せん断弾性係数(t=0)
および K0= E / 3(1 -2ν)、初期体積弾性係数(t=0)
gi、ki、τi
G、τi
K は i 番目のせん断弾性係数と体積弾性係数、およびそれらに対応する回数です。
材料の挙動に対する温度効果は、時間-温度対応原理により導入されます。この原理の数学式は、次のとおりです:
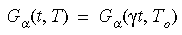
ここで、γt は換算時間、γ はシフト関数です。 この関数を近似化するため、WLF(Williams-Landel-Ferry)等式が使用されます:
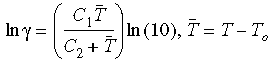
ここで、T0 は通常はガラス転移温度として選択される参照温度、C1 と C2 は材料依存定数です。
| パラメータ |
材料特性 |
|---|
| 線形弾性パラメータ |
X 方向の弾性係数(Elastic modulus in X)
|
|
XY 面内のポアソン比(Poisson's ratio in XY)
|
|
xy 面内のせん断弾性係数(Shear modulus in XY)
|
| 緩和関数パラメータ |
せん断緩和係数(Shear relaxation modulus)(1 ~ 8) (一般化 Maxwell モデル等式で g1、g2、...、g8 を表します)
|
|
時間値(せん断緩和係数 1 ~ 8)(一般化 Maxwell モデル等式で τ1
g、τ2
g、...、τ8
g を表します) |
|
体積緩和係数(Bulk Relaxation Modulus)(1 ~8) |
|
時間値(体積緩和係数 1 ~ 8)(一般化 Maxwell モデル等式で τ1
k、τ2
k、...、τ8
k を表します) |
| WLF 等式パラメータ
|
ガラス転移温度
(WLF 等式で T0 を表します)
|
|
Williams-Landel-Ferry 数式の第 1 定数
(WLF 等式で C1 を表します)
|
|
Williams-Landel-Ferry 数式の第 2 定数
(WLF 等式で C2 を表します)
|
せん断緩和曲線または体積緩和曲線をテーブル&カーブ(Tables & Curves)タブで定義する場合、t1 時間における曲線の最初の点は G1 係数または K1 係数になります。時間 t = 0 のとき、プログラムは自動的に G0 または K0 を弾性係数とポアソン比から計算します。
粘弾性材料モデルは、固体および厚肉シェル要素のドラフト精度、または高精度を使用できます。
粘弾性材料モデルを使用するとき、時間は非線形解析の実際の値です。