不規則振動環境で動作する構成部品の疲労損傷評価は、応答応力パワー スペクトル密度(PSD)関数の統計プロパティに基づく周波数領域で推定されます。
構造構成部品または機械構成部品が不規則荷重にさらされるとき(風力荷重下の風力タービン、波荷重下のオフショア構造、異なる路面プロファイルで動作する自動車のエンジンなど)、疲労寿命推定は周波数領域内で行われます。
振動疲労(または振動に基づく疲労)とは、荷重と応答(応力歪み履歴)がランダム プロセスであり、パワー スペクトル密度(PSD)関数などの統計的手段を使用してもっともよく記述される疲労寿命の推定のことです。
応答応力 PSD の統計的特性は、PSD 関数のモーメントによって取得できます。
| PSD の統計的特性 |
関係式 |
| 周波数 f (Hz)での応力 PSD S(f) の n 番目のスペクトル モーメント。 |
 (関係式 1) (関係式 1)
|
| 連続固定ガウス過程 σ の RMS(root-mean-square)値。 |
 (関連式 2) (関連式 2)
|
| 標準 1 秒サンプルの上向きゼロ交差 E[0] の平均数。 |
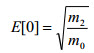 (関係式 3) (関係式 3)
|
| 標準 1 秒サンプルのピーク E[p] の平均数。 |
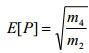 (関係式 4) (関係式 4)
|
| 不規則性係数 γ は 0 ~ 1 の間で変化します。応力信号がナロー バンド プロセスに近づくと、1 に近づきます(サイン波 γ = 1 の場合)。応力信号がホワイト ノイズ プロセスに近づくと、0.745 に収束します。 |
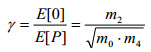 (関連式 5) (関連式 5)
または
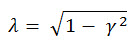 (関連式 6) (関連式 6)
|
材料疲労プロパティは、通常、S-N 曲線から得られます。これは、応力範囲 S (これは、引張時の最大繰り返し応力から圧縮時の最小繰り返し応力までの応力変化です)と平均破損サイクル数の間の関係を定義します。
最高サイクル疲労問題(N >= 104)の場合、S-N 曲線は単純化された形式で表すことができます。
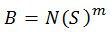 (関連式 7)
(関連式 7)
B および m は荷重および環境条件によって変化する材料プロパティであり、疲労テスト試験によって決定されます。
不規則荷重からの疲労による累積的損傷 E[AD] は Palmgren-Miner のルールに基づき、次のように表すことができます。
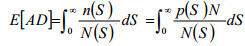 (関連式 8)
(関連式 8)
n(S) は応力範囲レベル S で適用されるサイクルの数であり、p(S) は応力範囲の確率密度関数です。 前の関連式における単純化された S-N 曲線の関連式を置き換えると、不規則応力応答からの疲労損傷の一般的な関係式は次から得られます。
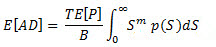 (関連式 9)、T は不規則荷重の継続時間(秒単位)です。
(関連式 9)、T は不規則荷重の継続時間(秒単位)です。
関連式 9 に基づいて 3 種類の疲労損傷推定方法を使用できます。 Steinberg の 3 バンド方法、ナロー バンド方法、Wirsching の方法です。 各方法は、確率密度関数 p(S) の定義が異なります。
ナロー バンド方法
ナロー バンド方法では、ナロー バンド信号のピークの確率密度関数は、レーリー分布になる傾向があります(Bendat J.S.、Probability Functions for Random Responses。 NASA report on Contact NASA-5-4590、1964)。
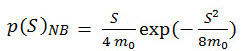 (関連式 10)
(関連式 10)
(関連式 10)を(関連式 9)に代入して積分すると、疲労損傷推定は次のような式になります。
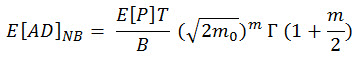 (関連式 11)、Γ(.) はガンマ関数です。
(関連式 11)、Γ(.) はガンマ関数です。
Wirsching の方法
Wirsching の方法(Wirsching、P.H.、Paez、T.L.、および Ortiz K.、Random Vibration、John Wiley & Sons Inc.、New York、1995)は、ナロー バンド方法を実験的補正係数で修正して、ワイド バンド プロセスを考慮します。
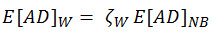 (関連式 12)
(関連式 12)
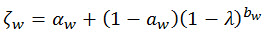 (関連式 13)
(関連式 13)
ζw はモンテカルロ シミュレーションから導出される実験的係数であり、さまざまなスペクトル密度関数を含みます。
αw および bw は、以下で与えられる最良適合パラメータです。
 (関連式 14)
(関連式 14)
Steinberg の 3 バンド方法
Steinberg の方法の仮定は、不規則応力応答の確率密度関数はガウス分布に従い、したがって応力応答強度の予想される値は特定の確率レベルで制限されるというものです。
- 応力サイクルの強度が応力応答信号の二乗平均平方根の 2 倍の範囲を超えない確率は 68.27% です。
- 応力サイクルの強度が応力応答信号の二乗平均平方根の 4 倍の範囲を超えない確率は 27.1% です。
- 応力サイクルの強度が応力応答信号の二乗平均平方根の 6 倍の範囲を超えない確率は 4.3% です。
二乗平均平方根の 6 倍より大きい範囲では応力サイクルは発生しません。
予想される疲労損傷は以下によって与えられます。
 (関連式 15)
(関連式 15)
Simulation では、応力 PSD 関数は、疲労試験の基になっているダイナミック - ランダム振動試験からの結果です。 vonMises 応力成分は、3 つのすべての方法の疲労による予測された損傷の計算と見なされます。