Cuándo utilizar el análisis dinámico
Los estudios estáticos suponen que las cargas son constantes o se aplican muy lentamente hasta que alcanzan sus valores completos. Debido a esta suposición, la velocidad y aceleración de cada partícula del modelo se supone nula. Como resultado, los estudios estáticos desprecian las fuerzas de inercia y amortiguación.
Para muchos casos prácticos, las cargas no se aplican lentamente ni cambian con el tiempo o la frecuencia. Para esos casos, utilice un estudio dinámico. Como regla general, si la frecuencia de una carga es mayor que 1/3 de la frecuencia más baja (fundamental), debe utilizarse un estudio dinámico.
Los estudios dinámicos lineales se basan en los estudios de frecuencia. El software calcula la respuesta del modelo mediante la acumulación de la contribución de cada modo al entorno de carga. En la mayoría de los casos, sólo los modos más bajos contribuyen significativamente a la respuesta. La contribución de un modo depende del contenido, magnitud, dirección, duración y ubicación de la frecuencia de la carga.
Los objetivos de la realización de un análisis dinámico incluyen:
Diseñar sistemas estructurales y mecánicos para funcionar sin errores en entornos dinámicos.
Modificar las características del sistema (geometría, mecanismos de amortiguamiento, propiedades de material, etc.) para reducir los efectos de la vibración.
Ecuaciones de movimiento
Sistemas de un grado de libertad (SDOF)
Considere el sistema sencillo de resorte de masa. La masa (m) está sujeta a una fuerza F(t) en la dirección u como una función del tiempo. Sólo se permite que la masa se mueva en la dirección u y, por tanto, éste es un sistema de un grado de libertad (SDOF). Un resorte de rigidez (k) resiste el movimiento.
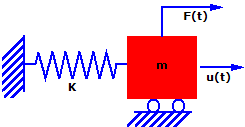
Si escribimos la segunda ley de Newton (fuerza es igual a masa por aceleración) para este sistema en el momento (t) da como resultado:
F(t)-ku(t) = mu..(t)
o:
mu..(t) + ku(t) = F(t)
donde:
u..(t) es la aceleración de la masa en el momento (t) y es igual a la segunda derivada de u con respecto al tiempo
k = es la rigidez del resorte
En teoría, si la masa se desplaza y se suelta, continuará vibrando con la misma amplitud. Sin embargo, en la práctica, la masa vibra con amplitudes progresivamente más pequeñas hasta que se detiene. Este fenómeno se denomina amortiguamiento y está originado por una pérdida de energía mediante fricción y otros efectos. El amortiguamiento es un fenómeno complejo. Para los fines de esta explicación, suponemos que la fuerza de amortiguamiento es proporcional a la velocidad. Este tipo de amortiguamiento se llama amortiguamiento viscoso.
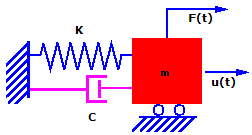
Si tenemos en cuenta el amortiguamiento, la ecuación anterior se convierte en:
mu..(t) + cu.(t) + ku(t) = F(t)
donde:
u.(t) es la velocidad de la masa en el momento (t) y es igual a la primera derivada de u con respecto al tiempo
Nota: En estudios estáticos, la velocidad y aceleración son tan pequeñas que pueden despreciarse, y F y u no son funciones del tiempo. La ecuación se reduce a: F=ku.
Sistemas de múltiples grados de libertad (MDOF)
Para un sistema de múltiples grados de libertad (MDOF), m, c y k son matrices en lugar de valores únicos, y las ecuaciones de movimiento se expresan así:
 , donde:
, donde:
[M]: matriz de masa
[K]: matriz de rigidez
[C]: matriz de amortiguamiento
{u(t)}: vector de desplazamiento en el momento t (componentes de desplazamiento de cada nodo)
 vector de aceleración en el momento t (componentes de aceleración de cada nodo)
vector de aceleración en el momento t (componentes de aceleración de cada nodo)
 vector de velocidad en el momento t (componentes de velocidad de cada nodo)
vector de velocidad en el momento t (componentes de velocidad de cada nodo)
{f(t)}: vector de carga dependiente del tiempo (componentes de fuerza de cada nodo)
Temas relacionados
Análisis estático lineal frente a análisis dinámico lineal
Cargas dinámicas
Cargas y opciones de resultados para análisis dinámicos