Modèles de fluage
Le fluage est une déformation dépendant du temps et résultant d'une contrainte constante. Il se manifeste dans la plupart des matériaux techniques, notamment dans les métaux soumis à des températures élevées, les plastiques à haut polymère, le béton et les propulseurs à poudre. Comme les effets du fluage mettent longtemps à apparaître, ils sont généralement négligés dans les analyses dynamiques.
La courbe de fluage est un diagramme traçant la déformation par rapport au temps. On peut distinguer trois régimes dans une courbe de fluage, à savoir les régimes primaire, secondaire et tertiaire (voir la figure ci-dessous). Ce sont les régimes primaire et secondaire qui présentent généralement un intérêt.
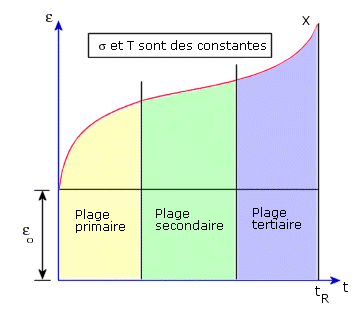
Deux lois de fluage reposant sur une approche d'équation d'état ont été mises en place. Chacune d'elles définit une expression pour la déformation de fluage uniaxial en termes de contrainte uniaxiale et du temps.
Loi de puissance classique pour le fluage (loi de Bailey-Norton)
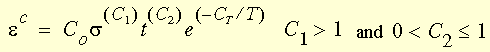
où :
T = Température (Kelvin) (= température d'entrée + température de référence + température de décalage)
C
T = Une constante de matériau définissant la dépendance du fluage vis-à-vis de la température
C0 est la constante de fluage 1 que vous saisissez dans l'onglet Propriétés de la boîte de dialogue Matériau.
Les unités de la constante de fluage 1 doivent être saisies dans le système d'unités SI. Le facteur de conversion est égal à 1/ (contrainte ^ (C1) * temps^(C2)). Les unités des contraintes sont en N/m2 et le temps est en secondes.
C1 est la constante de fluage 2 et C2 est la constante de fluage 3 dans la boîte de dialogue de propriétés du matériau.
La loi de puissance classique pour le fluage représente les régimes de fluage primaire et secondaire en une seule formule. Le régime de fluage tertiaire n'est pas pris en compte. “t” représente le temps réel courant (et non pseudo) et sigma représente la contrainte uniaxiale totale au temps t.
Pour appliquer ces lois au comportement de fluage multiaxial, les hypothèses suivantes sont posées :
-
La loi de fluage uniaxial est toujours valide si la déformation de fluage uniaxial et la contrainte uniaxiale sont remplacées par leurs valeurs efficaces.
-
Le matériau est isotropique
-
Les déformations de fluage sont incompressibles
Dans le cas d'une analyse de fluage numérique, où le chargement cyclique peut être appliqué conformément à la règle de durcissement de déformation, les taux de déformation de fluage actuels sont exprimés comme une fonction de la contrainte en cours et du fluage total :
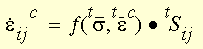
où :
