Modèle de plasticité de von Mises

Les critères d'élasticité peuvent être exprimés ainsi :

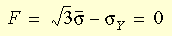
où s représente la contrainte effective et s Y la contrainte d'élasticité des tests uniaxiaux. Le modèle de von Mises peut être utilisé pour décrire le comportement des métaux. Lors de l'utilisation de ce modèle de matériaux, vous devez tenir compte des points suivants :

• On suppose une plasticité à faible déformation lorsque des petits ou des grands déplacements sont utilisés.

• Une hypothèse de règle de flux associé est formulée.

• Des règles d'écrouissage cinématique et isotropique sont disponibles. Une combinaison linéaire d'écrouissage isotropique et cinématique est faite lorsque le rayon et le centre de la surface de plastification dans l'espace déviatorique varient tous deux en fonction de l'historique du chargement.

Le paramètre RK définit la proportion de l'écrouissage cinématique et isotropique.

Dans le cas d'un écrouissage isotropique pur, le paramètre RK a la valeur 0. Le rayon de la surface de plastification augmente, mais son centre reste fixe dans l'espace déviatorique.

Dans le cas d'un écrouissage cinématique pur, le paramètre RK a la valeur 1. Le rayon de la surface de plastification reste constant, mais son centre peut se déplacer dans l'espace déviatorique.

• Une courbe contrainte-déformation uniaxiale bilinéaire ou multi-linéaire pour la plasticité peut être saisie. Pour la définition d'une courbe contrainte-déformation bilinéaire, la limite et le module d'élasticité sont saisis dans la boîte de dialogue Matériau . Pour la définition d'une courbe contrainte-déformation multi-linéaire, une courbe contrainte-déformation doit être définie.

• Lorsque vous définissez une courbe contrainte-déformation, le premier point de la courbe doit être le point d'élasticité du matériau. Les propriétés de matériau telles que le module élastique, la limite d'élasticité, etc. seront prélevées de la courbe contrainte-déformation si disponible et non du tableau des propriétés de matériaux dans la boîte de dialogue Matériau. Seul le coefficient de Poisson (NUXY) sera retenu du tableau.

La définition des courbes de contrainte-déformation n'est pas prise en charge par les études de test de chute.

• Pour la description de courbe contrainte-déformation bilinéaire, la limite et le module d'élasticité peuvent être associés aux courbes de température pour exécuter l'analyse thermoplastique.

• Il est recommandé d'utiliser la méthode itérative NR (Newton-Raphson).

Le modèle Huber-von Mises peut être utilisé avec des éléments volumiques (qualité moyenne et supérieure) et des éléments à coque épaisse (qualité moyenne et supérieure).

La thermoplasticité n'est pas disponible avec les éléments coque.

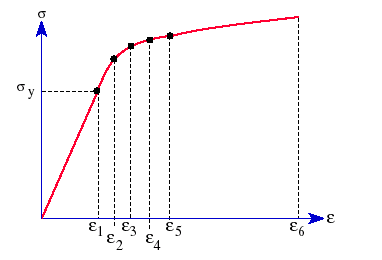
La figure suivante décrit une courbe contrainte-déformation type d'un matériau en plastique :

Analyse des grandes déformations

Dans le cadre d'une plasticité à grande déformation, la mesure logarithmique de la déformation est définie ainsi :

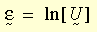
où U représente le tenseur de traction droite généralement obtenu à partir de la décomposition polaire droite du gradient de déformation F (à savoir, F = R U, R représentant le tenseur de rotation). La déformation logarithmique incrémentielle est estimée ainsi :

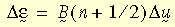
où B (n+1/2) représente la matrice de contrainte-déplacement estimée au pas de simulation n+1/2 et D u le vecteur de déplacements incrémentiels. La forme ci-dessus est toutefois une approximation de deuxième ordre de la formule exacte.

Le ratio de contrainte est interprété comme celui de Green-Naghdi afin de rendre correctement le modèle constitutif indépendant du cadre ou objectif, en faisant passer le ratio de contrainte du système global au système R.

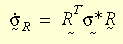
La forme du modèle constitutif entier sera identique à la théorie de la petite déformation. La théorie de la plasticité de grande déformation est appliquée au critère d'élasticité de von Mises, à la règle de flux associatif et au durcissement, soit isotropique soit cinématique (bilinéaire ou multi-linéaire). La propriété de matériau dépendant de la température est prise en charge par le durcissement bilinéaire. L'algorithme radial-retour est utilisé dans le cas courant. L'idée principale consiste à calculer approximativement le vecteur normal N comme suit :

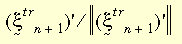
où,

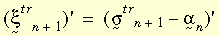
La figure suivante illustre les deux équations ci-dessus :

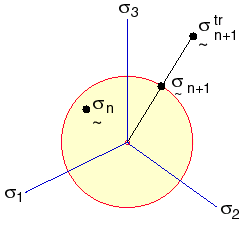
Le vecteur de force d'élément et les matrices de raideur sont calculés en fonction de la formule lagrangienne actualisée. Les contraintes de Cauchy, les déformations logarithmiques et l'épaisseur courante (éléments à coque uniquement) sont enregistrées dans le fichier des résultats.

L'élasticité dans le cas présent est modélisée sous forme hyperélastique, qui suppose de petites déformations élastiques mais tient compte des grandes déformations en plastique. Pour les problèmes d'élasticité à grande déformation (tels que le caoutchouc), vous pouvez utiliser les modèles des matériaux hyperélastiques tels que Mooney-Rivlin.

La contrainte de Cauchy (vraie) et la déformation logarithmique doivent être utilisées dans la définition de la courbe contrainte-déformation multi-linéaire.

Comparaison entre les critères de plasticité de Tresca et de von Mises