Modèle hyperélastique de Mooney - Rivlin

La fonction de densité d'énergie de déformation de Mooney-Rivlin est exprimée ainsi :

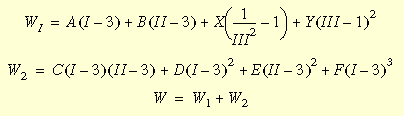
où I, II, et III sont des invariants du tenseur de déformation de Cauchy-Green et peuvent être exprimés en fonction des rapports d'étirements principaux ; A, B, C, D, E et F sont des constantes de matériaux de Mooney et

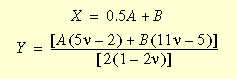
On a observé qu'au fur et à mesure qu'un matériau approche l'incompressibilité, le troisième invariant, III, s'approche de l'unité alors que Y s'approche de l'infini. Par conséquent, pour les valeurs de coefficient de Poisson proches de 0,5, le dernier terme dans w 1 reste solidaire et une solution peut être obtenue.

Le modèle de matériau de Mooney-Rivlin peut être utilisé avec des éléments volumiques et des coques épaisses. Les propriétés du matériau pour le modèle de Mooney-Rivlin sont spécifiées dans la boîte de dialogue Matériau. bsp;Vous pouvez saisir jusqu'à six constantes de Mooney-Rivlin : Mooney_A, Mooney_B, Mooney_C, Mooney_D, Mooney_E et Mooney_F.

Les constantes de Mooney-Rivlin sont automatiquement calculées lorsque l'option Utiliser les données de la courbe pour calculer les constantes du matériau est cochée dans la boîte de dialogue Matériau . Les constantes sont enregistrées dans un fichier texte avec l'extension .log dans le dossier de résultats actif de l'étude.

REMARQUES

• Utilisez la méthode itérative NR (Newton-Raphson).

• Les valeurs du coefficient de Poisson supérieures ou égales à 0,48 mais inférieures à 0,5 sont acceptables. Lorsque la formulation de déplacement-pression est utilisée, le coefficient de Poisson est recommandé dans la plage de 0,499 à 0,4999.

• Les matériaux de type caoutchouc se déforment en principe rapidement sous l'action de chargements de faible intensité, requérant ainsi un chargement initial lent.

• Lorsque vous utilisez des matériaux de type caoutchouc, en raison du comportement hautement non linéaire du problème, une augmentation rapide du chargement entraîne souvent soit une instabilité numérique (termes diagonaux négatifs dans la raideur), soit une divergence pendant les itérations d'équilibre. L'algorithme d'incrémentation adaptative automatique peut s'avérer utile dans de tels cas.

• Le déplacement ou le contrôle en longueur d'arc peut s'avérer plus efficace que le contrôle de la force lorsque des termes diagonaux négatifs se produisent systématiquement sous divers taux de chargement.

• Pour les éléments de coque ayant une formulation épaisse, l'analyse est simplifiée puisque l'incompressibilité n'entraîne pas des termes non solidaires. La formulation est dérivée en supposant une incompressibilité parfaite (coefficient de Poisson de 0,5) et par conséquent le coefficient NUXY est négligé.

• Les constantes A et B doivent être définies de telle sorte que (A+B) > 0. Pour de plus amples informations sur la détermination des valeurs des constantes A et B, référez-vous aux travaux de Kao et Razgunas.

Pour définir des modèles hyperélastiques...