Nell'Analisi statica lineare, i carichi vengono applicati gradualmente e lentamente fino a raggiungere una magnitudine completa. A questo punto, i carichi rimangono costanti (non variano nel tempo). Le accelerazioni e le velocità del sistema eccitato sono negligenti, quindi nessuna forza d'inerzia e di smorzamento viene considerata nella formula:

dove:
[K] : matrice di rigidezza
{u}: vettore di spostamento
{f}: vettore di carico
La soluzione produce spostamenti, sollecitazioni che sono costanti.
In Analisi dinamica lineare, i carichi applicati sono dipendenti dal tempo. I carichi possono essere deterministici (periodici, non periodici) o non deterministici e cioè non possono essere esattamente previsti ma possono essere descritti statisticamente. Le accelerazioni e le velocità del sistema eccitato sono significative, quindi nessuna forza d'inerzia e di smorzamento viene considerata nella formula:
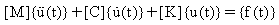
dove:
[K] : matrice di rigidezza
[C] : matrice di smorzamento
[M]: matrice di massa
{u(t)}: vettore di spostamento che varia nel tempo
 : vettore di accelerazione che varia nel tempo
: vettore di accelerazione che varia nel tempo
 : vettore di velocità che varia nel tempo
: vettore di velocità che varia nel tempo
{f(t)}: vettore di carico che varia nel tempo
Il responso del sistema è dato in termini di cronologia (ampiezze vs tempo) o in termini di range di frequenza (frequenza vs valori massimi).
Per l'analisi dinamica lineare, la massa, la rigidezza e le matrici di smorzamento non variano nel tempo.
Le proprietà del materiale sono considerate lineari. Gli studi dinamici non lineari devono essere usati se esiste la non linearità del materiale.
In generale, si possono considerare le condizioni statiche se la frequenza dei carichi è molto più bassa della più bassa frequenza naturale del sistema.