La matrice di smorzamento simmetrico n x n [C] è formulata come una combinazione lineare delle matrici di massa [M] e rigidità [K]:
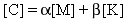(Equazione 1)
-
Coefficiente Alpha: imposta il coefficiente proporzionale alla massa α.
-
Coefficiente Beta: imposta il coefficiente proporzionale alla rigidezza β.
Il tipo di smorzamento descritto da (Equazione 1) è conosciuto come Rayleigh o smorzamento proporzionale.
Questa forma di [C] è ortogonale rispetto ai vettori eigen del sistema.
Applicando la trasformazione delle coordinate modali, la matrice di smorzamento modale [c] diventa diagonale:
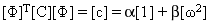(Equazione 2)
Lo smorzamento Rayleigh può essere definito per gli studi dinamici lineari e non lineari.
Relazione dei coefficienti Rayleigh e rapporto di smorzamento modale
La matrice di smorzamento modale [c] è data da:
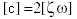(Equazione 3)
Il coefficiente di smorzamento viscoso ci per la modalità ith viene calcolata in questo modo:
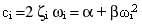(Equazione 4),
e il rapporto di smorzamento viscoso ζi viene espresso con
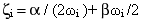(Equazione 5)
Se i rapporti di smorzamento dalla modalità ith e jth sono ζi e ζj, i coefficienti Rayleigh α e β saranno calcolati dalla soluzione delle due equazioni algebriche:
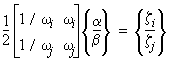(Equazione 6)
Se entrambe le modalità hanno lo stesso rapporto di smorzamento ( ζi = ζj = ζ) , i valori di α e β sono dati da:
(Equazione 7)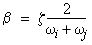 
(Equazione 8)
Il rapporto di smorzamento viscoso ζ per qualsiasi altra modalità varia con la frequenza nel modo illustrato nella figura:
