Typická křivka závislosti mezi napětím a namáháním nelineárního modelu materiálu vypadá takto:

V případě vývoje napětí vzhledem k poměrnému zatížení, kde se složky tenzoru napětí mění vzájemně v konstantním poměru, je možné vyjádřit namáhání v rámci konečného stavu napětí následujícím způsobem:

Ds je sečná matice materiálu, Es je sečný modul a v je Poissonova konstanta
Pro začlenění tohoto modelu by měla být definována Poissonova konstanta a křivka závislosti napětí a namáhání materiálu.
Vektor celkového namáhání ε se použije pro výpočet efektivního namáhání ε(bar) a tak se získá sečný modul z uživatelem definované křivky závislosti mezi napětím a namáháním materiálu. V trojrozměrném případě:

Křivka závislosti mezi napětím a namáháním ze třetího (tlakového) do prvního (tahového) kvadrantu je pro tento model u dvojrozměrných a trojrozměrných elementů použitelná s několika úpravami. Sečný modul materiálu a tečný modul materiálu se získá pomocí metody interpolace. Pokud definujeme poměr R, který je funkcí objemového namáhání Φ, efektivního namáhání a Poissonovy konstanty, existuje pro R následující vztah:
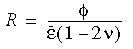
Upozorňujeme, že R = 1 představuje případ jednoosého tahu a R = -1 případ tlaku. Tyto dva případy jsou dány jako horní a dolní hranice; když hodnota R tyto hodnoty přesáhne, program ji vrátí do mezních hodnot. Nelineární elastický model materiálu lze použít u objemových sítí a sítí skořepin.