Système à un degré unique de liberté (SDOF)
Examinez le système masse-ressort simple. La masse (m) est soumise à une force F(t) dans la direction u, comme fonction du temps. La masse peut seulement se déplacer dans la direction u, et il s'agit donc d'un système à un seul degré de liberté (SDOF). Un ressort de raideur (k) s'oppose au mouvement.

L'écriture de la seconde loi de Newton (la force est égale à la masse multipliée par l'accélération) pour ce système au moment (t) aboutit à:
F(t)-ku(t) = mu..(t)
ou:
mu..(t) + ku(t) = F(t)
où :
u..(t) est l'accélération de la masse au moment (t) et est égal à la deuxième dérivée de u par rapport au temps.
k = est la raideur du ressort
En théorie, si la masse est déplacée et relâchée, elle continuera à vibrer à la même amplitude indéfiniment. En pratique, la masse vibre à des amplitudes progressivement plus petites jusqu'à ce qu'elle s'arrête. Ce phénomène est appelé amortissement et est provoqué par la perte d'énergie due à la friction et à d'autres effets. L'amortissement est un phénomène complexe. Dans le cadre de notre discussion, supposez que la force d'amortissement est proportionnelle à la vitesse. Ce type d'amortissement est appelé amortissement visqueux.

En considérant l'amortissement, l'équation ci-dessus devient:
mu..(t) + cu.(t) + ku(t) = F(t)
où :
u..(t) est la vitesse de la masse au moment (t) et est égal à la première dérivée de u par rapport au temps.
Dans les études statiques, la vitesse et l'accélération sont si faibles qu'elles peuvent être négligées et F et u ne sont pas des fonctions du temps. L'équation ci-dessus se réduit à: F=ku.
Système à plusieurs degrés de liberté (SDOF)
Pour un système à plusieurs degrés de liberté (MDOF), m, c et k deviennent des matrices à la place de valeurs uniques et les équations de mouvement sont exprimées sous la forme :
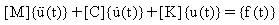
où :
[M] : matrice de masse
[K]: matrice de raideur
[C]: matrice d'amortissement
{u(t)}: vecteur de déplacement au temps t (composants de déplacement de chaque nœud)
 : vecteur d'accélération au temps t (composants d'accélération de chaque nœud)
: vecteur d'accélération au temps t (composants d'accélération de chaque nœud)
 : vecteur de vitesse au temps t (composants de vitesse de chaque nœud)
: vecteur de vitesse au temps t (composants de vitesse de chaque nœud)
{f(t)}: vecteur de chargement variable dans le temps (composants de force de chaque nœud)