Le système d'équations de mouvement d'un système linéaire à n degrés de liberté excité par une force variable dans le temps est:
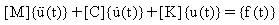 (Equation 1)
(Equation 1)
où :
[M] = n x n matrice d'inertie symétrique
[C] = n x n matrice d'amortissement symétrique
[K] = n x n matrice de raideur symétrique
{f(t)} = vecteur de force à n dimensions
{u},  et
et  sont les vecteurs à n dimensions de déplacement, de vitesse et d'accélération, respectivement.
sont les vecteurs à n dimensions de déplacement, de vitesse et d'accélération, respectivement.
(Equation 1) est un système de n équations différentielles ordinaires simultanées à coefficients constants. Les équations de mouvement sont couplées au moyen de termes de masse, de raideur et d'amortissement. Le couplage dépend du système de coordonnées utilisé pour décrire mathématiquement les équations de mouvement.
Le concept de base sous-tendant l'analyse modale est la transformation du système couplé de (Equation 1) en un ensemble d'équations indépendantes en utilisant la matrice modale [Φ] comme matrice de transformation. [Φ] contient les modes normaux {f}i pour i = 1, ....,n organisés comme suit :
 (Equation 2)
(Equation 2)
Les modes normaux et les valeurs propres du système sont dérivés de la solution du problème de valeur propre:
 (Equation 3)
(Equation 3)
où [ω2] est une matrice diagonale du carré des fréquences propres.
Dans le cas des systèmes linéaires, le système de n équations de mouvement peut être découplé en n équations à un seul degré de liberté en termes du vecteur de déplacement modal {x}:
 (Equation 4)
(Equation 4)
La substitution du vecteur {u} depuis (Eq.4) et sa pré-multiplication par [Φ]T (Equation 1) aboutit à :
 (Equation 5)
(Equation 5)
Les modes normaux satisfont la propriété d'orthogonalité et la matrice modale [Φ] est normalisée pour satisfaire aux équations suivantes:
 (Equation 6)
(Equation 6)
 (Equation 7) et
(Equation 7) et
 (Equation 8).
(Equation 8).
En substituant(Equations.6--8), (Equation 5) devient un système de n équations différentielles de second ordre SDOF indépendantes:
 pour i =1, ..., n (Equation 9)
pour i =1, ..., n (Equation 9)
(Equation 9) est résolue en utilisant des méthodes d'intégration étape par étape telles que les méthodes Wilson-thêta et Newmark.
L'intégration est effectuée dans le domaine temporel où les résultats de la dernière étape sont utilisés pour prédire ceux de la suivante.
Le vecteur de déplacement (u) du système est dérivé de (Equation 4).