Dans l'analyse statique linéaire, les chargements sont appliqués lentement et progressivement jusqu'à l'intensité désirée. Une fois cette intensité atteinte, les chargements restent constants dans le temps. Les accélérations et vitesses du système excité sont négligeables; par conséquent, aucune force d'inertie ou d'amortissement n'est prise en compte dans la formule:
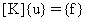
où :
[K]: matrice de raideur
{u} : vecteur de déplacement
{f} : vecteur de chargement
La solution produit des déplacements et des contraintes qui sont constants.
Dans l'analyse dynamique linéaire, les chargements appliqués dépendent du temps. Les chargements peuvent être déterministes (périodiques ou apériodiques) ou non déterministes, ce qui veut dire qu'ils ne peuvent pas être prédits précisément, mais peuvent être décrits statistiquement. Les accélérations et vitesses du système excité sont siginificatives; par conséquent, les forces d'inertie et d'amortissement doivent être prises en compte dans la formule:
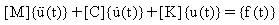
où :
[K]: matrice de raideur
[C]: matrice d'amortissement
[M] : matrice de masse
{u(t)}: vecteur de déplacement variant dans le temps
 : vecteur d'accélération variant dans le temps
: vecteur d'accélération variant dans le temps
 : vecteur de vitesse variant dans le temps
: vecteur de vitesse variant dans le temps
{f(t)}: vecteur de chargement variant dans le temps
La réponse du système est donnée en termes d'évolution dans le temps (amplitudes par rapport au temps) ou en termes de gammes de fréquences (valeurs maximales par rapport à la fréquence).
Dans le cas de l'analyse dynamique linéaire, les matrices de masse, de raideur et d'amortissement ne varient pas avec le temps.
Les propriétés des matériaux sont supposées être linéaires. S'il existe des matériaux non linéaires, ce sont les études dynamiques non linéaires qui doivent être utilisées.
De façon générale, vous pouvez supposer des conditions statiques si la fréquence des chargements est beaucoup plus petite que la plus petite fréquence propre du système.