Nitinolün genellikle sonlu gerinimlere dayanma kabiliyeti için kullanılması nedeniyle, bu model için güncellenen Lagrangian formülasyonuyla birlikte logaritmik gerinimlerden yararlanan büyük gerinim teorisi kullanılmaktadır.
Dolayısıyla bünye modeli, logaritmik gerinimleri ve Kirchhoff gerilim bileşenlerini ilişkilendirecek şekilde yapılandırılır. Bununla birlikte, sonuç olarak bünye matrisi ve gerilim vektörünün her ikisi de mevcut Cauchy (gerçek) gerilimlerine dönüştürülür.

|
σs
t1, σf
t1
|
Çekme yüklemesi için İlk ve Nihai akma gerilimi [SIGT_S1, SIGT_F1]
|
|
σs
t2, σf
t2
|
Çekme boşaltması için İlk ve Nihai akma gerilimi [SIGT_S2, SIGT_F2]
|
|
σs
c1, σf
c1
|
Sıkıştırma yüklemesi için İlk ve Nihai akma gerilimi [SIGC_S1, SIGC_F1]
|
|
σs
c2, σf
c2
|
Sıkıştırma boşaltması için İlk ve Nihai akma gerilimi [SIGC_S2, SIGC_F2]
|
|
eul
|
(Maksimum Çekme Plastik Gerinimi) *(3/2)0,5
|
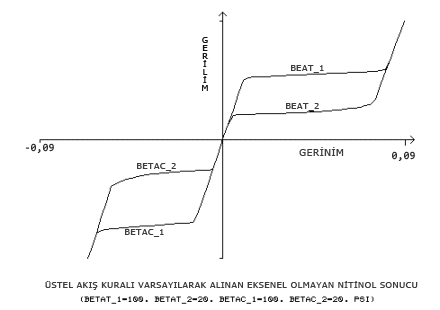
Üstel akış kuralı, β
t1, β
t2, β
c1, β
c2 ek girdi sabitlerini kullanır:
|
βt1
|
malzeme parametresi, çekme yüklemesi için dönüşüm hızını ölçer, [BETAT_1]
|
|
βt2
|
malzeme parametresi, çekme boşaltması için dönüşüm hızını ölçer, [BETAT_2]
|
|
βc1
|
malzeme parametresi, sıkıştırma yüklemesi için dönüşüm hızını ölçer, [BETAC_1]
|
|
βc2
|
malzeme parametresi, sıkıştırma boşaltması için dönüşüm hızını ölçer, [BETAC_2]
|
Akma Kriteri
Faz dönüşümünün basınca bağımlılık olasılığını modellemek amacıyla, akma kriteri için bir Drucker-Prager tipi yükleme fonksiyonu kullanılır:
F(τ) = sqrt(2)*σ(bar) + 3*α*p
F - RI
f = 0
Burada;
σ(bar) = etkili gerilim
p = ortalama gerilim (veya hidrostatik basınç)
α = sqrt(2/3) (σsc1 - σst1 ) / (σsc1 + σst1)
Rf
I = [ σf
I(sqrt(2/3) + α)], I = yükleme için 1 ve boşaltma için 2'dir