A la différence des matériaux isotropiques, les matériaux orthotropiques ont des directions de force préférées mutuellement perpendiculaires. Les propriétés le long de ces directions (dites aussi directions principales) sont des valeurs extrêmes des coefficients d'élasticité.
La matrice [D] d'un matériau orthotrope a neuf propriétés élastiques indépendantes. Il y a également trois propriétés pour la dilatation thermique.
Relations de contrainte-déformation orthotropiques en deux dimensions
En 2D, les relations de contrainte-déformation orthotropiques peuvent être exprimées comme suit en incluant les effets de température :
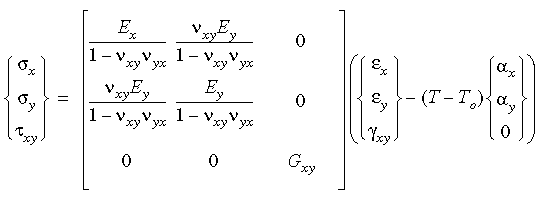
Pour satisfaire la symétrie dans la matrice des modules d'élasticité, νxy Ey = νyx Ex.
Vous devez satisfaire la condition de symétrie précédente lorsque vous saisissez des valeurs numériques du module d'élasticité ou du coefficient de Poisson.
En outre, si vous ne saisissez pas la valeur numérique du module de cisaillement, le programme la calcule comme indiqué ci-dessous :
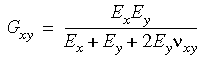
En 3D, les conditions de symétrie orthotropiques stipulent ce qui suit :
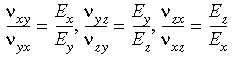
Lorsque vous saisissez les propriétés des matériaux orthotropiques en 3D, vous devez vous assurer que les conditions de symétrie ci-dessus sont remplies.
Si vous saisissez des valeurs numériques pour les modules de cisaillement (Gxy, Gyz et Gxz), le programme utilise ces valeurs (même si elles ne sont pas compatibles avec les conditions de symétrie orthotrope).
Remarquez que, si vous ne saisissez pas la valeur numérique du module de cisaillement, le programme la calcule comme indiqué ci-dessous :
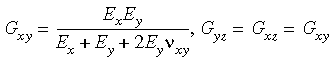
Si Ex = Ey = Ez, le programme calcule les modules de cisaillement en interne, mais s'ils sont explicitement définis.
Le programme utilise 0,0 pour les coefficients de Poisson qui ne sont pas explicitement définis.