En los análisis estáticos lineales, las cargas se aplican lenta y gradualmente hasta que alcanzan sus magnitudes completas. A continuación, las cargas permanecen constantes (sin variación en el tiempo). Las aceleraciones y velocidades del sistema excitado son insignificantes y, por tanto, no se tienen en cuenta fuerzas de inercia o amortiguamiento en la fórmula:
donde:
[K] : matriz de rigidez
{u}: vector de desplazamiento
{f}: vector de carga
La solución produce desplazamientos y tensiones que son constantes.
En los estudios dinámicos lineales, las cargas aplicadas son dependientes del tiempo. Las cargas pueden ser deterministas (periódicas y no periódicas) o no deterministas (no pueden predecirse con precisión pero sí pueden describirse desde un punto de vista estadístico). Las aceleraciones y velocidades del sistema excitado son considerables y, por tanto, se deben tener en cuenta fuerzas de inercia o amortiguamiento en la fórmula:
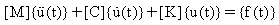
donde:
[K] : matriz de rigidez
[C] : matriz de amortiguamiento
[M]: matriz de masa
{u(t)}: vector de desplazamiento dependiente del tiempo
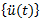: vector de aceleración dependiente del tiempo
: vector de velocidad dependiente del tiempo
{f(t)}: vector de carga dependiente del tiempo
La respuesta del sistema se proporciona en términos de historiales de tiempo (amplitudes frente a tiempo) o en términos de espectros de frecuencia (valores pico frente a frecuencia).
Para análisis dinámicos lineales, las matrices de masa, rigidez y amortiguamiento no varían con el tiempo.
Se supone que las propiedades de material son lineales. Deben utilizarse los estudios dinámicos no lineales si existe no linealidad de material.
En general, puede suponer condiciones estáticas si la frecuencia de las cargas es considerablemente menor que la frecuencia natural más baja del sistema.