Elastische Materialien, die die Fähigkeit haben, die mechanische Energie aufgrund von Viskositätseffekten zu verteilen, werden als viskoelastische Materialien bezeichnet.
Bei mehrachsigen Spannungszuständen kann der konstitutive Zusammenhang wie folgt ausgedrückt werden:

Zeichenerklärung: e(bar) und φ sind die deviatorische und volumetrische Dehnung, G(t - τ) und K(t - τ) sind Schub- und Umgebungsentspannungsfunktionen.
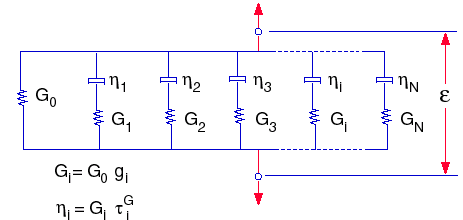
Die Entspannungsfunktionen können dann durch das mechanische Modell dargestellt werden, das gewöhnlich als verallgemeinertes Maxwell-Modell bezeichnet wird und die folgenden Ausdrücke aufweist:

Zeichenerklärung: G0 = E / 2(1+ ν), anfänglicher Schubmodul (t = 0)
und K0= E / 3(1 -2ν), anfänglicher Kompressionsmodul (t = 0)
gi, ki, τi
G und τi
K sind die i-ten Schub- und Kompressionsmodule und zugehörigen Zeiten.
Die Auswirkung der Temperatur auf das Materialverhalten wird durch das Zeit-Temperatur-Korrespondenzprinzip berücksichtigt. Die mathematische Form dieses Prinzips lautet:

wobei γt die reduzierte Zeit und γ die Versatzfunktion ist. Die WLF-Gleichung (Williams-Landel-Ferry) dient zur Annäherung der Funktion:

Dabei ist T0 die Referenztemperatur, die in der Regel als Glasübergangstemperatur verwendet wird; C1 und C2 sind materialabhängige Konstanten.
| Parameter |
Materialeigenschaft |
|---|
| Linear elastische Parameter |
Elastizitätsmodul in x
|
|
Poissonsche Zahl in xy
|
|
Schubmodul in xy
|
| Entspannungsfunktionsparameter |
Schubrelaxationsmodul (1 bis 8) (stellen g1, g2, ..., g8 in den Gleichungen des verallgemeinerten Maxwell-Modells dar)
|
|
Zeitwerte (Schubrelaxationsmodul 1 bis 8) (stellt τ1
g, τ2
g, ... , τ8
g in den verallgemeinerten Maxwell-Modell-Gleichungen dar) |
|
Kompressionsrelaxationsmodul (1 bis 8) |
|
Zeitwerte (Kompressionsrelaxationsmodul 1 bis 8) (stellt τ1
k, τ2
k, ... , τ8
k in den verallgemeinerten Maxwell-Modell-Gleichungen dar) |
| WLF-Gleichungsparameter
|
Glasübergangstemperatur
(stellt T0 in der WLF-Gleichung dar)
|
|
Erste Konstante für Williams-Landel-Ferry-Gleichung
(stellt C1 in der WLF-Gleichung dar)
|
|
Zweite Konstante für Williams-Landel-Ferry-Gleichung
(stellt C2 in der WLF-Gleichung dar)
|
Wenn Sie eine Schub- oder Umgebungsrelaxationskurve auf der Registerkarte Tabellen & Kurven definieren, ist der erste Punkt der Kurve der G1 - oder K1-Modul zur Zeit t1. Zur Zeit t = 0 berechnet das Programm automatisch G0 oder K0 aus dem Elastizitätsmodul und der Poissonschen Zahl.
Das viskoelastische Materialmodell kann für Volumenkörper- und dickwandige Wandungselemente mit hoher und Entwurfsqualität verwendet werden.
Zeit hat in der nicht-linearen Analyse bei Verwendung des viskoelastischen Materialmodells reale Werte.