Use inertial relief to calculate stresses and deformations on a free body that is accelerating such as a rocket being propelled by its engine, an aircraft in flight, or a moving automobile.
If a model is not adequately restrained, a small force can cause rigid body motion. Even in cases when the applied forces are balanced, a small unbalanced force can result from numerical approximations.
To activate inertial relief, select Use inertial relief in the Static dialog box. When this option is checked, the program automatically applies inertia forces distributed to all nodes of the model to form an equivalent state of static equilibrium.
When you activate the inertial relief option, you can solve structural problems without having to apply restraints or activate the soft spring option to stabilize the model against rigid body motions.
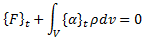
|
{F}t
|
Applied external forces
|
|
{α}t
|
Translational acceleration due to inertia (to be calculated)
|
|
ρ
|
Material density
|
|
v
|
Material volume
|
The above equation can be represented as:
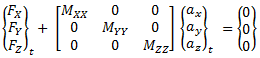
where Mxx, Myy and Mzz are total masses in x, y and z directions and are evaluated
by a row-by-row summation of the elemental mass matrices over the translational
degrees of freedom. Once Mxx, Myy, and Mzz are evaluated, the equation
yields the induced accelerations αx, αy, and αz which are applied as an
acceleration field to the solution.
Inertial relief is also applied to cases where an unbalanced external force on an elastic body can cause rigid body motion. The unbalanced force can be balanced
by distributed inertia forces induced by a translational acceleration field. It is not recommended to activate the inertial relief option to balance gravity, centrifugal, or thermal loads as this could cause erroneous results.
The inertial relief option is particularly useful when you import loads from SOLIDWORKS Motion where external loads can be slightly unbalanced. Inertial relief is based on D'Alembert's principle, which states that one can transform an accelerating rigid body into an equivalent static system by adding inertial forces and inertial torque or moment.
In the Simulation application, only the translational field is considered; any induced rotations
are ignored.