Check this option to instruct the program to add soft springs to prevent instability. If you apply loads to an unstable design, it will translate and/or rotate as a rigid body. You should apply adequate restraints to prevent rigid body motion.
To add soft springs, select Use soft spring to stabilize model in the Static dialog box
If you cannot stabilize the design by applying adequate restraints, select this option to add soft springs and rerun the analysis. Animating the resulting deformed shape will show you excessive motion in one or more directions. You can then apply appropriate restraints to prevent rigid body motion.
The addition of soft springs increases the global stiffness of the model. It is advisable, after applying the proper restraints, to repeat the analysis without activating the soft spring option.
A rigid (free) body mode of a structure represents motion without internal deformations.
In structural analysis, rigid body modes arise due to either insufficient or
nonexistent constraints imposed on the structure. However, there are analysis
problems where the imposition of constraints is not desirable, yet the deformable
behavior of the structure under loads is of interest.
For example, you may
come across a stress analysis problem where an equilibrium state is maintained
by the applied loads, thus requiring no constraints. Ordinarily, for such problems
the program will execute unsuccessfully, indicating a message about singular stiffness matrix. However, if you specify the option for soft spring addition, the
program will automatically add a small stiffness to the diagonal terms of the
structural stiffness matrix as shown below, enabling numerical stability during
solution:
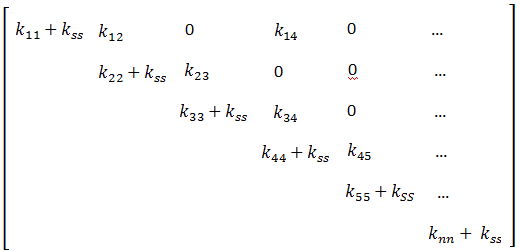
where kss denotes the stiffness added due to the soft spring option.
Singular stiffness matrices are also encountered due to ill-posed problems, for example
models with very low or highly disproportionate elastic moduli and section properties.
This option is automatically applied for contact problems solved by the Direct Sparse solver.
The treatment of rigid body modes in the analysis of natural frequencies can be
accomplished in two ways: by using the soft spring option outlined above, or
by using the shift option in eigenvalue extraction.