Die Blatz-Ko Spannungsenergiedichte-Funktion ist bei der Modellierung komprimierbarer Gummiarten (polyurethanschaumartig) von Nutzen und kann wie folgt ausgedrückt werden:
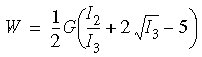
Zeichenerklärung:
- G = E / 2(1+ν) ist der Schubmodul unter Infinitesimalverformungen, E ist der Elastizitätsmodul, v ist die Poissonsche Zahl.
- Ik (k = 1,..3) sind die Invarianten des Cauchy-Green-Verformungstensors C = Ik ©)
- C = 2ε +I , ε ist der Lagrange-Dehnungstensor und I ist die Identitätsmatrix.
Der obige Ausdruck enthält nur eine Materialkonstante G. Da v = 0,25 für das Blatz-Ko-Modell ist, wird der Elastizitätsmodul als einzige Materialeigenschaft berücksichtigt.
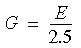
Das Blatz-Ko-Modell wird derzeit nur von Volumenkörperelementen (Entwurfsqualität und hohe Qualität) unterstützt.
Das ausgewählte Blatz-Ko-Modell ist eine vereinfachte Form der von Blatz und Ko (1962) erstellten Gleichung, die die Verformung eines stark komprimierbaren Polyurethanschaumgummis modelliert. Die Spannungsenergie wurde anhand folgender Gleichung geschätzt:

Dabei gilt Folgendes:

Eine spezielle Form dieser Drei-Parameter-Familie von elastischem Potenzial wurde später vorgeschlagen, wobei für die Konstanten α, β und ν die folgenden Werte angenommen wurden: α = 0,5, β = 0 und ν = 0,25.