阻尼效果

如果您在動態系統中套用了初始條件，系統振動的振幅會逐漸減少直到靜止為止。此現象稱作阻尼。阻尼是一種複雜的現象，它會藉由許多機制使能量消失，例如內部與外部摩擦、在細微等級時循環彈性延伸材料的熱效應，以及空氣阻力。

以數學方式描述散熱機制並不容易。阻尼效果通常由理想化的數學公式所表示。在許多情況中，阻尼效果可由同等的黏滯性阻尼器適當地描述。

黏滯性阻尼器 (或稱減震器) 可產生與速度成正比的力。可在充滿黏性液體 (例如機油) 汽缸內自由移動的活塞是黏滯性阻尼器的一個例子。阻尼力 F_d 已假設為與位於阻尼器兩端的相對速度線性相關：

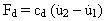(方程式 1)。

常數 c_d，為曲線的斜度 F_d 與相對速度，稱為黏性阻尼的係數；

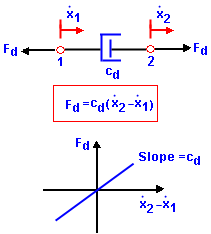
黏性阻尼的係數單位為(力)/(速度) 或 (力 x 時間)/(長度)。

一般黏性阻尼 n 自由度系統的回應計算公式如下：

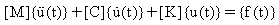(方程式 2)

其中：

[M] = n x n 對稱質量 (或慣性) 矩陣

[C] = n x n 對稱阻尼矩陣

[K] = n x n 對稱勁度矩陣

{f(t)} = n-因次力向量

{u}、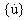 和 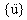分別是位移、速度與加速度 n-因次向量。

一般而言，傳統的形式分析並不一定會導致動作方程式的獨立系統，除非可以將由於形式座標轉換而產生的阻尼矩陣 [c] 視為對角矩陣。

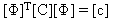(方程式 3)