單一自由度 (SDOF) 系統
考量簡易質量彈力系統。質量 (m) 會承受 u 方向的力 F(t) 而成為時間函數。僅允許質量以 u 方向移動,因此這是一個單一自由度 (SDOF) 系統。動作會受到勁度彈力 (k) 的抵抗
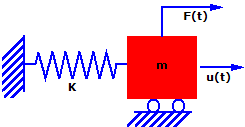
在時間 (t) 為此系統寫入牛頓第二定律 (力等於質量乘以加速度) 會產生:
F(t)-ku(t) = mu..(t)
或:
mu..(t) + ku(t) = F(t)
其中:
u..(t) 是時間 (t) 時的質量的加速度,它等於相對於時間的 u 的第二個衍生值
k = 彈力的勁度
理論上,如果質量已經移動並且釋放時,它會繼續以相同的振幅永久振動。實際上,質量會逐漸以較小的振幅振動直到其靜止為止。此現象稱為阻尼,而它是透過摩擦以及其他效應產生的能量損失所造成。阻尼是一種複雜的現象。在這裡的討論中,我們假設阻尼力與速度成正比。這種阻尼類型稱為黏性阻尼。
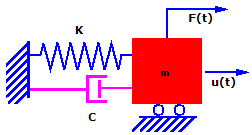
考慮阻尼時,上面的方程式會變成:
mu..(t) + cu.(t) + ku(t) = F(t)
其中:
u.(t) 是時間 (t) 時的質量的速度,它等於相對於時間的 u 的第一個衍生值
在靜態研究中,速度與加速度因為太小而能夠忽略,而 F 和 u 並不是時間函數。上面的方程式會縮減成:F=ku。
多重自由度 (MDOF) 系統
在多重自由度 (MDOF) 系統方面,m、c 和 k 會成為矩陣而非單一值,而動作方程式會以下列形式表示:
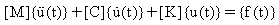
其中:
[M]:質量矩陣
[K]:勁度矩陣
[C]:阻尼矩陣
{u(t)}:時間 t 的位移向量(每個節點的位移零組件)
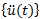 時間 t 的加速度向量 (每個節點的加速度組成)
時間 t 的加速度向量 (每個節點的加速度組成)
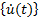 :時間 t 的速度向量 (每個節點的速度零組件)
:時間 t 的速度向量 (每個節點的速度零組件)
{f(t)}:隨時間變化的負載向量(每個節點的力零組件)