隨時間變化的力量所激發的線性 n-自由度系統的動作方程式系統為:
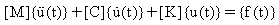 (方程式 1)
(方程式 1)
其中:
[M] = n x n 對稱質量慣性矩陣
[C] = n x n 對稱阻尼矩陣
[K] = n x n 對稱勁度矩陣
{f(t)} = n-因次力向量
{u}、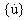 和
和 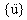 分別是位移、速度與加速度 n-因次向量。
分別是位移、速度與加速度 n-因次向量。
(方程式 1) 是包含常數係數的 n 個聯立常微分方程式的系統。動作方程式是透過質量、勁度和阻尼項式進行耦合的。耦合是根據在數學上用來描述動作方程式的座標系統而定。
形式分析背後的基本構想是使用形式矩陣 [Φ] 作為轉換矩陣,將 (方程式 1) 的耦合系統轉換成一組獨立方程式。[Φ] 包含正向模式 {f}i i = 1、....、n 排列如下:
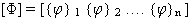 (方程式 2)
(方程式 2)
正向模式與系統的特徵值是衍生自特徵值問題的解答:
 (方程式 3)
(方程式 3)
其中 [ω2] 是自然頻率的對角矩陣。
在線性系統中,n 個動作方程式的系統可以重新耦合成為在形式位移向量 {x} 中的 n 單一自由度方程式:
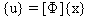 (方程式 4)
(方程式 4)
從 (方程式 4) 代入向量 {u} 並且將它預先乘以 [Φ]T (方程式 1) 降伏:
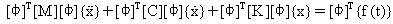 (方程式 5)
(方程式 5)
正向模式可滿足正交屬性,而形式矩陣 [Φ] 則會正規化以滿足下列方程式:
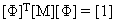 (方程式 6)
(方程式 6)
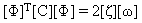 (方程式 7),和
(方程式 7),和
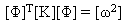 (方程式 8)。
(方程式 8)。
藉由代入 (方程式.6--8),(方程式 5) 成為 n 獨立 SDOF 二階式微分方程式的系統:
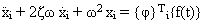 i =1、...、n (方程式 9)
i =1、...、n (方程式 9)
(方程式 9) 是使用例如 Wilson-Theta 和 Newmark 的逐步積分法解出的。
積分是在時域中執行的,其中最後步驟的結果是用於預測下一個步驟。
系統的位移向量 (u) 是衍生自 (方程式 4)。