隨機過程
隨機過程一般都會被檢視為一系列的隨機變數，或是可描述具體現象大量記錄數目。記錄可以是時間函數 {xk(t)} 或頻率 {xk(f)}。每個記錄與任何其他記錄多少都會有些不同。因此，在分析中包括所有可能的記錄就非常重要。而隨機過程則是在統計資料屬性中描述。隨機振動研究中的每個負載都是隨機過程。這些負載的模型回應也是在統計資料項式中描述的隨機過程。
自動相關性函數
隨機過程的自動相關性函數描述在不同時間的記錄值之間的相關性。它會定義為隨機變數產品的期望值 x(t)，包含本身的時移版本。
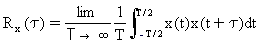(方程式 1)
均方根 (rms)
均方根的值提供與隨機過程有關的能量測量。
它定義為自動相關性函數 t = 0 的值
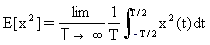(方程式 2)
其中，E 稱為期望運算子。平均值的正方根即稱為均方根或簡稱 rms。
變化
隨機過程的均方根與其平均 μx 有關。
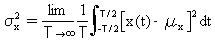(方程式 3)
變化的正方根稱為標準偏差。
功率頻譜密度 (psd)
功率頻譜密度已定義為隨機過程的自動相關性函數的傅立葉轉換。
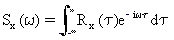(方程式 4)
功率頻譜密度描述隨機過程的能量如何在頻率域中分佈。
白色雜訊
白色雜訊訊號在所有頻率中有一致的功率頻譜密度。換句話說，訊號的能量在所有頻率中會平均分佈。