Expand EinführungEinführung
Expand VerwaltungVerwaltung
Expand BenutzeroberflächeBenutzeroberfläche
Expand Grundlagen von SolidWorksGrundlagen von SolidWorks
Expand Umsteigen von 2D auf 3DUmsteigen von 2D auf 3D
Expand BaugruppenBaugruppen
Expand CircuitWorksCircuitWorks
Expand KonfigurationenKonfigurationen
Expand SolidWorks CostingSolidWorks Costing
Expand Design CheckerDesign Checker
Expand Konstruktionsstudien in SolidWorksKonstruktionsstudien in SolidWorks
Expand Zeichnungen und DetaillierungZeichnungen und Detaillierung
Expand DFMXpressDFMXpress
Expand DriveWorksXpressDriveWorksXpress
Expand FloXpressFloXpress
Expand Importieren und ExportierenImportieren und Exportieren
Expand GroßkonstruktionGroßkonstruktion
Expand ModellanzeigeModellanzeige
Expand GussformkonstruktionGussformkonstruktion
Expand BewegungsstudienBewegungsstudien
Expand Teile und FeaturesTeile und Features
Expand LeitungsführungLeitungsführung
Expand BlechBlech
Collapse SimulationSimulation
Expand SimulationXpressSimulationXpress
Expand SkizzierenSkizzieren
Expand Sustainability ProdukteSustainability Produkte
Expand SolidWorks UtilitiesSolidWorks Utilities
Expand ToleranzenToleranzen
Expand ToolboxToolbox
Expand SchweißkonstruktionenSchweißkonstruktionen
Expand Workgroup PDMWorkgroup PDM
Expand ProblembehebungProblembehebung
Expand GlossarGlossar
Inhaltsverzeichnis ausblenden

Iterative Lösungsmethoden: Newton-Raphson-Schema (NR)

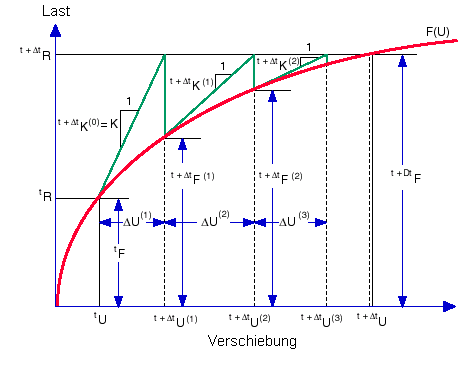
Bei diesem Schema wird die Matrix für die tangentiale Steifigkeit bei jeder Iteration innerhalb eines bestimmten Schritts gebildet und aufgelöst, wie in der folgenden Abbildung gezeigt. Die NR-Methode weist eine hohe Konvergenzrate auf. Die Konvergenzrate ist quadratisch. Da die tangentiale Steifigkeit bei jeder Iteration gebildet und aufgelöst wird, kann diese Methode bei großen Modellen jedoch unangemessen sein. Deshalb empfiehlt es sich möglicherweise, eine andere iterative Methode zu verwenden.

Siehe auch

Iterative Lösungsmethoden

Modifiziertes Newton-Raphson-Schema (MNR)



Feedback zu diesem Thema geben

SOLIDWORKS ist dankbar für Ihr Feedback zur Präsentation, Genauigkeit und Vollständigkeit der Dokumentation. Verwenden Sie das nachstehende Formular, um Ihre Kommentare und Vorschläge zu diesem Thema direkt an unser Dokumentations-Team zu senden. Das Dokumentations-Team kann keine Fragen für den technischen Support beantworten. Klicken Sie hier für Informationen zum technischen Support.

* Erforderlich

 
*E-Mail:  
Betreff:   Feedback zu Hilfethemen
Seite:   Iterative Lösungsmethoden: Newton-Raphson-Schema (NR)
*Kommentar:  
*   Ich bestätige, dass ich die Datenschutzerklärung, unter der meine personenbezogenen Daten durch Dassault Systèmes verarbeitet werden, gelesen habe und akzeptiere.

Thema drucken

Wählen Sie aus, was gedruckt werden soll:

x

Sie verwenden einen Browser, der älter als Internet Explorer 7 ist. Für eine optimierte Anzeige sollten Sie Ihren Browser auf Internet Explorer 7 oder höher aktualisieren.

 Diese Meldung nicht mehr anzeigen
x

Web-Hilfe Inhaltsversion: SOLIDWORKS 2012 SP05

Um die Web-Hilfe in SOLIDWORKS zu deaktivieren und stattdessen die lokale Hilfe zu verwenden, klicken Sie auf Help > SOLIDWORKS Web-Hilfe verwenden.

Um Probleme mit der Oberfläche und der Suche der Web-Hilfe zu melden, wenden Sie sich an Ihren Support vor Ort. Um Feedback zu einzelnen Hilfethemen zu geben, verwenden Sie den Link “Feedback zu diesem Thema” auf der entsprechenden Themenseite.

0.20.46