Creep Models
Creep is a time dependent strain produced under a state of constant
stress. Creep is observed in most engineering materials especially metals
at elevated temperatures, high polymer plastics, concrete, and solid propellant
in rocket motors. Since creep effects take long time to develop, they
are usually neglected in dynamic analysis.
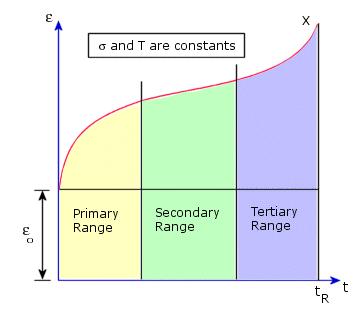
Creep curve is a graph between strain versus time. Three different regimes
can be distinguished in a creep curve; primary, secondary, and tertiary
(see the following figure). Usually primary and secondary regimes are
of interest.
Two creep laws based on an “Equation of State” approach are implemented.
Each law defines an expression for the uniaxial creep strain in terms
of the uniaxial stress and time.
Classical Power Law for Creep (Bailey-Norton law)
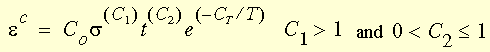
where:
T
= Temperature (Kelvin) (= input temperature + reference temperature +
offset temperature)
CT = A material constant defining the
creep temperature-dependency
The classical power law for creep represents primary and secondary creep
regimes in one formula. Tertiary creep regime is not considered. “t”
is the current real (not pseudo) time and s
is the total uniaxial stress at time t.
To extend these laws to multiaxial creep behavior, the following assumptions
are made:
For a numerical creep analysis, where cyclic loading may be applied,
based on the strain hardening rule, the current creep strain rates are
expressed as a function of the current stress and the total creep strain:
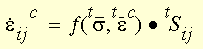
where:
