Viscoelastic Model
Elastic materials having the capacity to dissipate the mechanical energy
due to viscous effects are characterized as viscoelastic materials. For
multi-axial stress state, the constitutive relation can be written as:
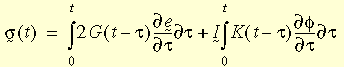
where e
and f
are the deviatoric and volumetric strains; G(t
- t) and K(t
- t) are shear and bulk relaxation functions.
The relaxation functions can then be represented by the mechanical model,
(shown in this figure)
which is usually referred to as a Generalized Maxwell Model having the
expressions as the following:
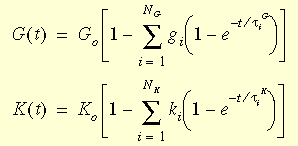
where G0 and K0 are the initial shear and bulk moduli
(t = 0) given by: G0 =
E/2(1+v) and
K0
=
E/3(1-2v).
gi,
ki,
tiG,
and tiK
are the i-th shear and bulk moduli and corresponding times.
The effect of temperature on the material behavior is introduced through
the time-temperature correspondence principle. The mathematical form of
the principle is:
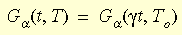
where g
t is the reduced time and g is the
shift function. The WLF (Williams-Landel-Ferry) equation is used to approximate
the function:
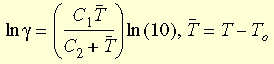
where TO is the reference temperature which is
usually picked as the Glass transition temperature; C1
and C2 are material dependent
constants.
The required parameters include the following:
|
Parameter |
Symbol |
Description |
|
Linear Elastic Parameters |
EX |
Elastic modulus |
|
NUxy |
Poisson's ratio |
|
GXY (optional) |
Shear modulus |
|
Relaxation Function Parameters |
G1, G2, G3,..., G8 |
represent g1, g2, ...,g8 in the Generalized Maxwell Model equations |
|
TAUG1, TAUG2, ....., TAUG8 |
represent t1g,
t2g,..., t8g
in the Generalized Maxwell Model equations |
|
K1, K2, ..., K8 |
represent k1, k2, ...,k8 in the Generalized Maxwell Model equations |
|
TAUK1, TAUK2, ..., TAUK8 |
represent t1k,
t2k,..., t8k
in the Generalized Maxwell Model equations |
|
WLF Equation Parameters |
REFTEMP |
represents T0 in the WLF equation |
|
VC1 |
represents C1 in the WLF equation |
|
VC2 |
represents C2 in the WLF equation |
When defining a shear or bulk relaxation curve
under the Tables & Curves
tab, the first point of the curve is the G1
or
K1
moduli
at time t1.
At time t = 0, the program automatically
computes G0
or
K0
from the Elastic modulus and Poisson's ratio.
The viscoelastic material model can be used with the draft and high
quality solid and thick shell elements.