Expand IntroductionIntroduction
Expand AdministrationAdministration
Expand User InterfaceUser Interface
Expand SolidWorks FundamentalsSolidWorks Fundamentals
Expand Moving from 2D to 3DMoving from 2D to 3D
Expand AssembliesAssemblies
Expand CircuitWorksCircuitWorks
Expand ConfigurationsConfigurations
Expand Design CheckerDesign Checker
Expand Design Studies in SolidWorksDesign Studies in SolidWorks
Expand Drawings and DetailingDrawings and Detailing
Expand DFMXpressDFMXpress
Expand DriveWorksXpressDriveWorksXpress
Expand FloXpressFloXpress
Expand Import and ExportImport and Export
Expand Large Scale DesignLarge Scale Design
Expand Model DisplayModel Display
Expand Mold DesignMold Design
Expand Motion StudiesMotion Studies
Expand Parts and FeaturesParts and Features
Expand RoutingRouting
Expand Sheet MetalSheet Metal
Collapse SimulationSimulation
Welcome to SolidWorks Simulation Online Help
Access to Help
Conventions
Legal Notices
Expand Analysis BackgroundAnalysis Background
Expand Simulation FundamentalsSimulation Fundamentals
Expand Simulation InterfaceSimulation Interface
Expand Simulation OptionsSimulation Options
Expand Simulation StudiesSimulation Studies
Expand Design StudiesDesign Studies
Expand 2D Simplification Study2D Simplification Study
Expand Composite ShellsComposite Shells
Expand Loads and RestraintsLoads and Restraints
Expand MeshingMeshing
Collapse Material PropertiesMaterial Properties
Assigning Materials
Applying a Material
Removing a Material
Expand Creating a Custom MaterialCreating a Custom Material
Creating a Material Library
Managing Favorite Materials
Using Drag and Drop to Define Materials
Material Properties Used in SolidWorks Simulation
Isotropic and Orthotropic Materials
Temperature - Dependent Material Properties
Defining Stress-Strain Curves
Expand Material Dialog BoxMaterial Dialog Box
Collapse Material ModelsMaterial Models
Material Models
Plasticity Drucker - Prager Model
Plasticity Tresca Model
Plasticity von Mises Model
Viscoelastic Model
Linear Elastic Orthotropic Model
Linear Elastic Isotropic Model
Hyperelastic Ogden Model
Hyperelastic Mooney - Rivlin Model
Nitinol Material Model
Nonlinear Elastic Model
Creep Models
Comparison of Tresca and von Mises Criteria for Plasticity
Generalized Maxwell Model
Hyperelastic Blatz - Ko Model
Expand ParametersParameters
Expand Analysis LibraryAnalysis Library
Expand Viewing ResultsViewing Results
Expand Study ReportsStudy Reports
Expand Checking Stress ResultsChecking Stress Results
Expand SimulationXpressSimulationXpress
Expand SketchingSketching
Expand Sustainability ProductsSustainability Products
Expand SolidWorks UtilitiesSolidWorks Utilities
Expand TolerancingTolerancing
Expand ToolboxToolbox
Expand WeldmentsWeldments
Expand Workgroup PDMWorkgroup PDM
Expand TroubleshootingTroubleshooting
Expand GlossaryGlossary
Hide Table of Contents

Nonlinear Elastic Model

For the particular case of stress history as related to proportional loading, where components of stress tensor vary monotonically in constant ratio to each other, the strains can be expressed in terms of the final state of stress in the following form:

where, Ds is the secant material matrix, Es is the secant modulus, and n is the Poisson's ratio. To incorporate this model, Poisson's ratio NUXY and a material stress-strain curve should be defined.

The total strain vector e is used to compute the effective strain e to get the secant modulus from the user-defined material (stress-strain) curve. For the three dimensional case,

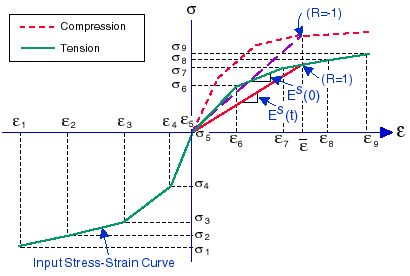
The stress-strain curve from the third (compressive) to the first (tensile) quadrants are applicable to this model for two and three dimensional elements with some modifications. A method of interpolation is used to get the secant and tangent material moduli. Defining a ratio R which is a function of the volumetric strain F, effective strain, and the Poisson's ratio, R has the following expression:

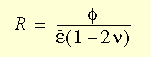
 It is noted that R = 1 represents the uniaxial tensile case and R = -1 is for the compressive case. These two cases are set to be the upper and lower bound such that when R exceeds these two values, the program will push it back to the limit. The nonlinear elastic material model can be used with solid and shell meshes.

The following is a typical stress-strain curve of a nonlinear material model:



Provide feedback on this topic

SOLIDWORKS welcomes your feedback concerning the presentation, accuracy, and thoroughness of the documentation. Use the form below to send your comments and suggestions about this topic directly to our documentation team. The documentation team cannot answer technical support questions. Click here for information about technical support.

* Required

 
*Email:  
Subject:   Feedback on Help Topics
Page:   Nonlinear Elastic Model
*Comment:  
*   I acknowledge I have read and I hereby accept the privacy policy under which my Personal Data will be used by Dassault Systèmes

Print Topic

Select the scope of content to print:
x

We have detected you are using a browser version older than Internet Explorer 7. For optimized display, we suggest upgrading your browser to Internet Explorer 7 or newer.

 Never show this message again
x

Web Help Content Version: SOLIDWORKS 2011 SP05

To disable Web help from within SOLIDWORKS and use local help instead, click Help > Use SOLIDWORKS Web Help.

To report problems encountered with the Web help interface and search, contact your local support representative. To provide feedback on individual help topics, use the “Feedback on this topic” link on the individual topic page.

0.20.20