Plasticity Tresca Model
This criterion is based on the assumption that in the state of yielding,
the maximum shearing stress at all points of a medium is the same, and
is equal to half of the yield stress that is obtained from a uniaxial
tension test for the given material.
In the three-dimensional case, yield occurs if at least one of the inequalities
is satisfied:
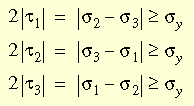
In other words, yielding is based on the maximum shearing stress which
is equal to half the difference between the maximum and minimum principal
stresses. Based on this criterion, the intermediate principal stress does
not influence the state of yielding.
Shearing Stress Intensity
The shearing stress intensity is defined by the square root of the second
invariant of the stress deviator and can be expressed as:
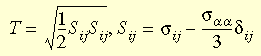
State of Pure Shear
The state of pure shear is defined as:
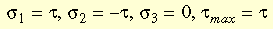
For this state, the shearing stress intensity and the maximum shearing
stress are equivalent:
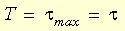
Using the Tresca conditions the shearing stress at the yield point is
obtained to be half of the tensile yield stress:

Based on the von Mises yield criterion the shearing yield stress is
equivalent to:
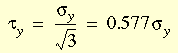
Notes
Both isotropic and
kinematic hardening rules are available for the Tresca model. A linear
combination of isotropic and kinematic hardening is implemented when both
the radius and the center of yield surface in deviatoric space can vary
with respect to the loading history.
The parameter RK defines the proportion of kinematic
and isotropic hardening.
For pure isotropic
hardening, the parameter RK has
the value 0. The radius of the yield surface expands but its center remains
fixed in deviatoric space.
For pure kinematic
hardening, the parameter RK has
the value 1. The radius of the yield surface remains constant while its
center can move in deviatoric space.'
Comparison of
Tresca and von Mises Criteria for Plasticity