Hyperelastic Mooney - Rivlin Model
The Mooney-Rivlin strain energy density function is expressed as:
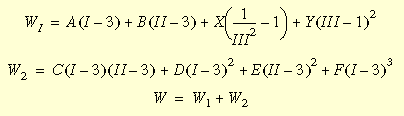
where I, II, and III are invariants of the right Cauchy-Green deformation
tensor and can be expressed in terms of principal stretch ratios; A, B,
C, D, E, and F are Mooney material constants, and
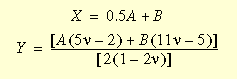
It has to be noted that as the material approach incompressibility,
the third invariant, III, approaches unity, while Y
approaches infinity. Thus, for values of Poisson's ratio close to 0.5,
the last term in w1 remains bounded, and a solution
can be obtained.
The Mooney-Rivlin material model can be used with solid elements and
thick shells. The material properties for Mooney-Rivlin model are input
in the Material dialog box. Up
to six Mooney-Rivlin constants can be input: Mooney_A, Mooney_B, Mooney_C,
Mooney_D, Mooney_E, and Mooney_F.
The Mooney-Rivin constants are automatically computed when the Use curve data to compute material constants
option in the Material
dialog box is checked. The constants are saved in a text file with the
extension .log in the active
result's folder for the study.
NOTES
Use the NR (Newton-Raphson)
iterative method.
Values of Poisson's ratio greater than or equal
to 0.48 but less than 0.5 are acceptable. When the displacement-pressure
formulation is used, Poisson's ratio is recommended in the range from
0.499 to 0.4999.
Rubber-like materials usually deform rapidly at
low magnitudes of loads thus requiring a slow initial loading.
When dealing with rubber-like materials, due to
the highly nonlinear behavior of the problem, rapid increase in loading
will often result in either numerical instability (negative diagonal terms
in the stiffness) or divergence during equilibrium iterations. The automatic-adaptive
stepping algorithm can help in such cases.
The displacement or the arc-length control may
prove to be more effective than force control when negative diagonal terms
repeatedly occur under various loading rates.
For shell elements with thick formulation, the
analysis is simplified since incompressibility does not result in unbounded
terms. The formulation is derived assuming perfect incompressibility (Poisson's
ratio of 0.5), and therefore NUXY is neglected.
Constants A and B must be defined such that (A+B)
> 0. For more information about how to determine the values of the
A and B constants, refer to the work by .
To
define hyper elastic models...