Hyperelastic Ogden Model
The Ogden strain energy density function, defined as,
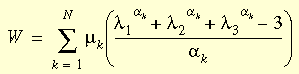
Where, l
i are the principal streches, a
i, m
i are material constants, and N is the number of terms in the function, is considered one of the most successful functions in describing the large deformation range of rubber-like materials. The penalty function used in the formulation of the Ogden model takes the form of the one used in Mooney-Rivlin model. The strain energy function actually used is a modified type of the Ogden function:
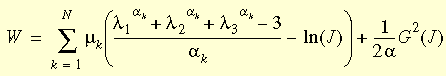
where J is the ratio of the deformed volume to the undeformed volume, N is the number of terms in the function, G(J)=J2 - 1 and
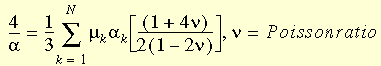
 3-term (modified Ogden) models are widely used. Up to 4 term models (N=4) are available in the program.
3-term (modified Ogden) models are widely used. Up to 4 term models (N=4) are available in the program.
Besides the material constants mentioned above, Poisson ratio is also required. For most cases, satisfactory results can be obtained by assigning Poisson's ratio from 0.49 to 0.499. Further, increasing Poisson's ratio will not have significant effect on the numerical results unless considerable volumetric strain is involved. When Poisson's ratio is extremely close to 0.5, it may cause solution termination due to negative diagonal terms in the stiffness matrix or lack of convergence.
The material properties for Ogden model are input through the Material dialog box. The required quantities are:
-
ALPH1, ALPH2, ALPH3, ALPH4,
-
MU1, MU2, MU3, MU4, and
-
NUXY
The Ogden model constants are automatically computed when the Use curve data to compute material constants option in the Material dialog box is checked. The constants are saved in a text file with the extension .log in the active result's folder for the study.
The Ogden model can be used with solid and shell elements with thick formulation.
To define hyper elastic models...