Viscoelastic Model
Elastic materials having the capacity to dissipate the mechanical energy due to viscous effects are characterized as viscoelastic materials. For multi-axial stress state, the constitutive relation can be written as:
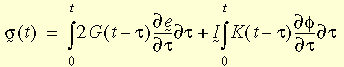
where e and f are the deviatoric and volumetric strains; G(t - t
) and K(t - t
) are shear and bulk relaxation functions. The relaxation functions can then be represented by the mechanical model, (shown in this figure
) which is usually referred to as a Generalized Maxwell Model having the expressions as the following:
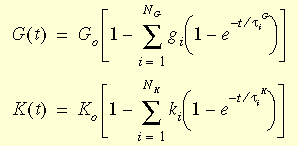
where G
0 and K
0 are the initial shear and bulk moduli (t = 0) given by: G
0
= E/2(1+v) and K
0
= E/3(1-2v).
g
i, k
i, t
i
G, and t
i
K are the i-th shear and bulk moduli and corresponding times.
The effect of temperature on the material behavior is introduced through the time-temperature correspondence principle. The mathematical form of the principle is:
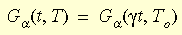
where g t is the reduced time and g is the shift function. The WLF (Williams-Landel-Ferry) equation is used to approximate the function:
where TO is the reference temperature which is usually picked as the Glass transition temperature; C1 and C2 are material dependent constants.
The required parameters include the following:
|
Parameter
|
Symbol
|
Description
|
|
Linear Elastic Parameters
|
EX
|
Elastic modulus
|
|
NUxy
|
Poisson's ratio
|
|
GXY (optional)
|
Shear modulus
|
|
Relaxation Function Parameters
|
G1, G2, G3,..., G8
|
represent g1, g2, ...,g8 in the Generalized Maxwell Model equations
|
|
TAUG1, TAUG2, ....., TAUG8
|
represent t1g, t2g,..., t8g in the Generalized Maxwell Model equations
|
|
K1, K2, ..., K8
|
represent k1, k2, ...,k8 in the Generalized Maxwell Model equations
|
|
TAUK1, TAUK2, ..., TAUK8
|
represent t1k, t2k,..., t8k in the Generalized Maxwell Model equations
|
|
WLF Equation Parameters
|
REFTEMP
|
represents T0 in the WLF equation
|
|
VC1
|
represents C1 in the WLF equation
|
|
VC2
|
represents C2 in the WLF equation
|
When defining a shear or bulk relaxation curve under the Tables & Curves tab, the first point of the curve is the G
1
or K
1
moduli at time t
1. At time t = 0, the program automatically computes G
0
or K
0 from the Elastic modulus and Poisson's ratio.
The viscoelastic material model can be used with the draft and high quality solid and thick shell elements.