Plasticity von Mises Model
The yield criterion can be written in the form:
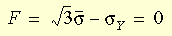
where s is the effective stress and s
Y is the yield stress from uniaxial tests. The von Mises model can be used to describe the behavior of metals. In using this material model, the following considerations should be noted:
-
Small strain plasticity is assumed when small displacement or large displacement is used.
-
An associated flow rule assumption is made.
-
Both isotropic and kinematic hardening rules are available. A linear combination of isotropic and kinematic hardening is implemented when both the radius and the center of yield surface in deviatoric space can vary with respect to the loading history.
The parameter RK defines the proportion of kinematic and isotropic hardening.
For pure isotropic hardening, the parameter RK has the value 0. The radius of the yield surface expands but its center remains fixed in deviatoric space.
For pure kinematic hardening, the parameter RK has the value 1. The radius of the yield surface remains constant while its center can move in deviatoric space.'
-
A bilinear
or multi-linear uniaxial stress-strain curve for plasticity can be input. For bilinear stress-strain curve definition, the yield strength and elastic modulus are input through the Material dialog box. For multi-linear stress-strain curve definition, a stress-strain curve should be defined.
-
When you define a stress-strain curve, the first point on the curve should be the yield point of the material. Material properties like elastic modulus, Yield strength, etc will be taken from the stress-strain curve when it is available and not from the material properties table in the Material dialog box. Only Poisson's ratio (NUXY) will be taken from the table.
 Defining stress-strain curves is not supported by drop test studies.
Defining stress-strain curves is not supported by drop test studies.
-
The yield strength and elastic modulus parameters for bilinear stress-strain curve description can be associated with temperature curves to perform thermoplastic analysis.
-
The use of NR (Newton-Raphson) iterative method is recommended.
The Huber-von Mises model can be used with the solid (draft and high quality) and thick shell (draft and high quality) elements.
 Thermo-plasticity is not available with shell elements.
Thermo-plasticity is not available with shell elements.
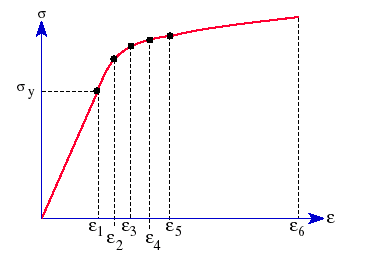
The following figure depicts a typical stress-strain curve of a plastic material:
Large Strain Analysis
In the theory of large strain plasticity, a logarithmic strain measure is defined as:
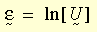
where U is the right stretch tensor usually obtained from the right polar decomposition of the deformation gradient F (i.e., F = R U, R is the rotation tensor). The incremental logarithmic strain is estimated as:
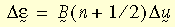
where B
(n+1/2) is the strain-displacement matrix estimated at solution step n+1/2 and D
u is the incremental displacements vector. It is noted that the above form is a second-order approximation to the exact formula.
The stress rate is taken as the Green-Naghdi rate so as to make the constitutive model properly frame-invariant or objective. By transforming the stress rate from the global system to the R-system,
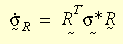
The entire constitutive model will be form-identical to the small strain theory. The large strain plasticity theory is applied to the von Mises yield criterion, associative flow rule and isotropic or kinematic hardening (bilinear or multi-linear). Temperature-dependency of material property is supported by bilinear hardening. The radial-return algorithm is used in the current case. The basic idea is to approximate the normal vector N by:
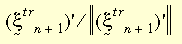
where,
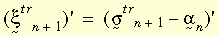
The following figure illustrates the above two equations.
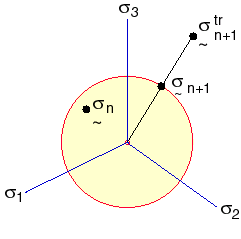
The element force vector and stiffness matrices are computed based on the updated Lagrangian formulation. The Cauchy stresses, logarithmic strains and current thickness (shell elements only) are recorded in the output file.
The elasticity in the current case is modeled in hyperelastic form that assumes small elastic strains but allows for arbitrarily large plastic strains. For large strain elasticity problems (rubber-like), you can use hyperelastic material models such as Mooney-Rivlin.
 Cauchy (true) stress and logarithmic strain should be used in defining the multi-linear stress-strain curve.
Cauchy (true) stress and logarithmic strain should be used in defining the multi-linear stress-strain curve.
Comparison of Tresca and von Mises Criteria for Plasticity