非線形解析を実施するためのさまざまな制御方法が考案されてきました。これらの制御方法は以下のように分類することができます。
荷重増分法(Incremental Load Control Method)
この方法では、システムに加えられた荷重を所定の変数として使用します。均衡経路上の各状態(ポイント)は、変形パラメータを決定する経路と面(F = 定数)との交点によって決定します。

この方法を有限要素解析に適用した場合は、荷重(基礎地盤振動、所定の変位、温度、重力など)は関連する「時間」カーブに従って蓄積されます。
変位増分法(Incremental Displacement Control Method)
この方法では、下の図に示すように、均衡経路上のポイントが、変形パラメータ(U = 定数)で定義された面とソリューション カーブとの交点によって決定します。

この方法を有限要素解析に組み込むと、加えた荷重のパターンが均等に増加(単一の荷重乗数を使用)して、指定した自由度の制御下で均衡を実現します。頂点または参照点を選択して指定した DOF が「時間」カーブに沿って増加します。
弧長増分法(Incremental Arc-Length Control Method)
この方法では、特殊なパラメータが、システムの均衡を制御する方程式に追加されたある制約方程式(補助方程式)を使って規定されます。幾何学的感覚では、この制御パラメータは下の図のように均衡経路の「円弧の長さ」として確認することができます。
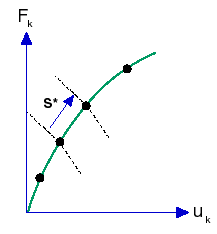
この方法を有限要素解析に組み込むと、加えた荷重のパターンが均等に増加(単一の荷重乗数を使用)して、指定した均衡経路の長さ(円弧の長さ)の制御下で均衡を実現します。円弧の長さは、プログラムによって自動的に計算されます。時間(time)カーブは必要ありません。
荷重増分法と変位増分法の両方が、次の図のように変化点(荷重増分法の場合はスナップ スルーとして、変位制御の場合はスナップ バックとして知られている)の近傍で制御不能になります。通常、これらの問題はフレーム、リング、およびシェルの座屈解析で見られます。弧長増分法がこれらの問題を解決します。
