Globalny układ współrzędnych
Kierunkowe dane wejściowe domyślnie odnoszą się do globalnego układu współrzędnych (X, Y i Z), bazującego na płaszczyźnie 1, którego początek zlokalizowany jest w początku układu współrzędnych części lub złożenia. Płaszczyzna1 jest pierwszą płaszczyzną, jaka pojawia się w drzewie operacji FeatureManager i może ona mieć inną nazwę. Triada odniesienia wskazuje kierunki globalne X, Y oraz Z.
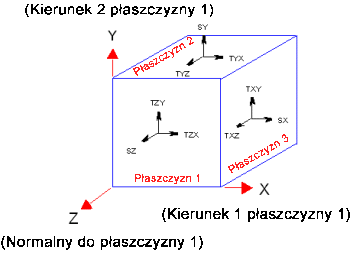
Poniższy rysunek ilustruje relację pomiędzy globalnym układem współrzędnych, a Płaszczyzną1, Płaszczyzną2 i Płaszczyzną3.

Gdzie: X jest Kierunkiem 1 Płaszczyzny 1, Y jest Kierunkiem 2 Płaszczyzny 1, a Z jest Normalna do Płaszczyzny 1.
|
|
Komponenty naprężenia w globalnym układzie współrzędnych
|
|
|
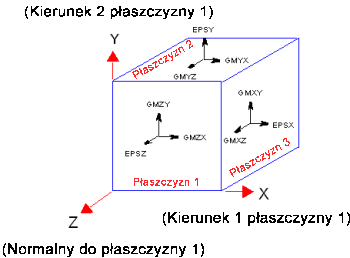
Komponenty odkształcenia w globalnym układzie współrzędnych
|
Globalny układ współrzędnych można wyświetlić na dowolnym wykresie klikając jego ikonę i wybierając Osie.
Lokalne układy współrzędnych
Lokalne układy współrzędnych są układami współrzędnych innymi od globalnego układu współrzędnych. Można określać umocowania i obciążenia w dowolnym żądanym kierunku. Na przykład: podczas definiowania siły na ścianie cylindrycznej, można ją stosować w kierunku promieniowym, okrężnym lub osiowym. W takim przypadku konieczne jest, aby wybrać oś jako geometrię odniesienia.
Podobnie w przypadku wybrania ściany sferycznej — w celu zastosowania umocowania można wybrać kierunek promieniowy, długości geograficzne lub szerokości geograficzne.
Podczas przeglądania również można używać osi i płaszczyzn odniesienia. Na przykład: można przeglądać naprężenia na ścianie cylindrycznej w kierunku promieniowym.
Używanie osi i płaszczyzn odniesienia. Osi i płaszczyzn odniesienia można użyć w celu zdefiniowania ortotropowych właściwości materiału bądź zastosowania kierunkowych obciążeń lub umocowań.
-
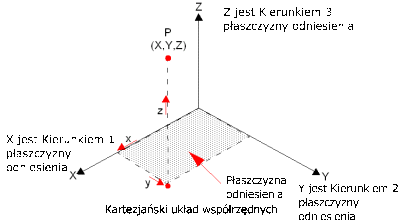
Używanie płaszczyzn odniesienia. Płaszczyzna odniesienia definiuje kartezjański układ współrzędnych, zgodnie z ilustracją.
-
Używanie osi odniesienia. Oś odniesienia definiuje cylindryczny układ współrzędnych, zgodnie z ilustracją.
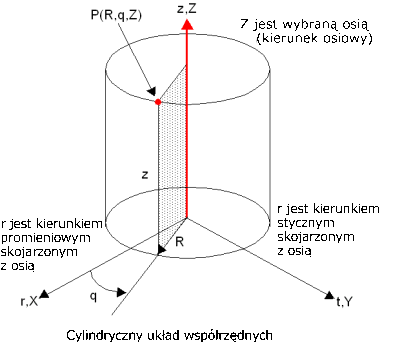
Szczegółowe informacje zawiera temat Obciążenia i umocowania.