Soustava rovnic pohybu v lineárním systému s n stupni volnosti buzeném časově proměnnou silou je:
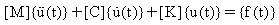(rovnice 1)
Pomocí transformace souřadnic se soustava n souběžných rovnic zjednoduší na n nezávislých rovnic (každou rovnici lze řešit samostatně):
pro r = 1, 2, ...., n (rovnice 2)
kde xr(t) jsou modální souřadnice související s uzlovými souřadnicemi ur(t) podle:
(rovnice 3).
Vektor modálního zatížení {m(t)} je dán tímto vztahem:
(rovnice 4).
Za předpokladu, že je buzení vyjádřeno funkcemi psd (power spectral density), lze řešení formulovat ve frekvenční doméně. Pokud je matice buzení psd dána jako [Sf(ω)], je matice psd modální síly definována jako:
(rovnice 5).
Psd reakce modálního posunutí [Sx(ω)] se získá ze vztahu:
(rovnice 6),
kde [H(ω)] představuje matici funkce modálního převodu a [H*(ω)] je jeho komplexně sdružené číslo. U normálních režimů je matice funkce převodu úhlopříčná s úhlopříčnými elementy Hr(ω)
(rovnice 7) a
(rovnice 8).
Psd reakce posunutí [Su(ω)] se následně odvodí z rovnice 3.
(rovnice 9).
Psd reakcí rychlosti a zrychlení vyjadřují tyto vztahy:
(rovnice 10) a
(rovnice 11).
Psd modální rychlosti a zrychlení souvisí s psd modálního posunu podle těchto vztahů:
(rovnice 12) a 
(rovnice 13)
Rovnici 10 a rovnici 11 lze přepsat takto:
(rovnice 14) a 
(rovnice 15).
Reakce modální autokorelace s nulovým zpožděním (τ=0) v rámci psd modální reakce se počítají z integrálů:
(rovnice 16)
(rovnice 17)
(rovnice 18).
Z předchozích rovnic se střední kvadratická reakce určí z úhlopříčných členů matic:
(rovnice 19),
(rovnice 20),
(rovnice 21).
Střední kvadratická odezva napětí
Napětí elementů {σ} jsou určena z uzlových posunutí {u} pomocí následujícího vztahu:
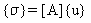(rovnice 22) nebo v rámci modálních posunutí {x} podle následujícího vztahu:
(rovnice 23), kde [Φ] je matice vlastních vektorů (eigenvectors).
Matice korelace napětí [Rσ] je dána následujícím vztahem:
(rovnice 24).